Чему равна площадь трапеции? Трапеция это важная и часто исследуемая геометрическая фигура в курсе геометрии, начиная с 7 класса. В процессе обучения школьники учатся решать задачи по геометрии на нахождение боковых сторон и оснований трапеции, углов и средней линии. Важно уметь находить периметр и площадь трапеции. Рассмотрим чему равна площадь трапеции и решим несколько задач на нахождение площади трапеции.
Содержание
Как найти площадь произвольной трапеции
Площадь трапеции ![]() равна произведению полусуммы её оснований на высоту трапеции.
равна произведению полусуммы её оснований на высоту трапеции.
![]()
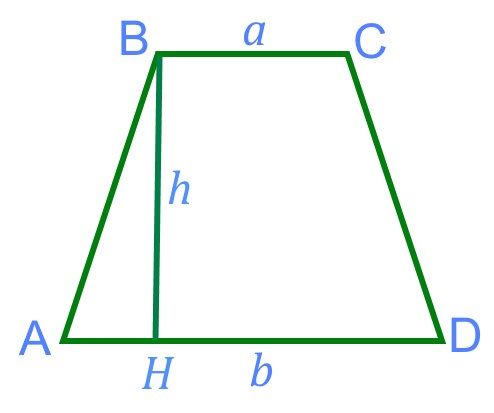
Единицей измерения площади является квадратная единица длины: м2, см2, кв.ед., км2.
Докажем, что данная формула верна для любой трапеции.
Доказательство 1
Пусть нам дана трапеция ![]() , проведем из вершины
, проведем из вершины ![]() высоту трапеции
высоту трапеции ![]() на сторону
на сторону ![]() .
.
Продлим сторону ![]() на длину основания
на длину основания ![]() получим точку
получим точку ![]() . Продлим сторону
. Продлим сторону ![]() трапеции
трапеции ![]() на длину стороны
на длину стороны ![]() . Получим точку
. Получим точку ![]() .
.
Соединим точки ![]() и
и ![]() . Трапеция
. Трапеция ![]() равна трапеции
равна трапеции ![]() по построению.
по построению.
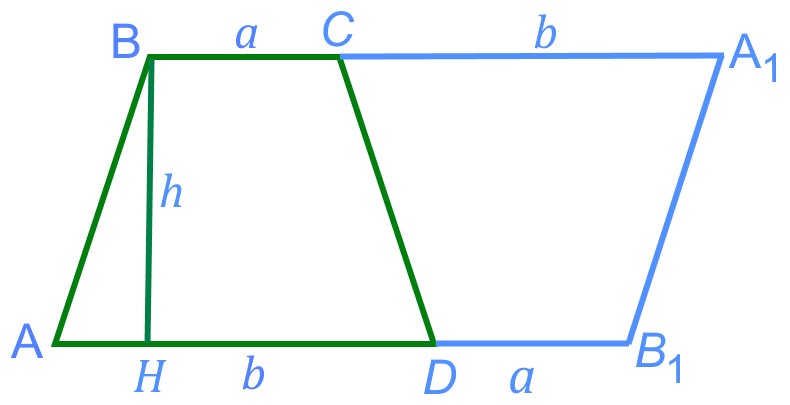
Полученный в результате построения четырехугольник ![]() — параллелограмм, площадь которого равна двум площадям трапеции
— параллелограмм, площадь которого равна двум площадям трапеции ![]() :
:
![]()
Отсюда площадь трапеции
![]()
так как ![]() , то получим:
, то получим:
![]() .
.
Таким образом, ![]() .
.
Что и требовалось доказать.
Доказательство 2
Достроим трапецию ABCD до прямоугольника, получим прямоугольник ![]() .
.
Площадь трапеции ![]() можно получить, если вычесть из площади прямоугольника площади достроенных треугольников.
можно получить, если вычесть из площади прямоугольника площади достроенных треугольников.
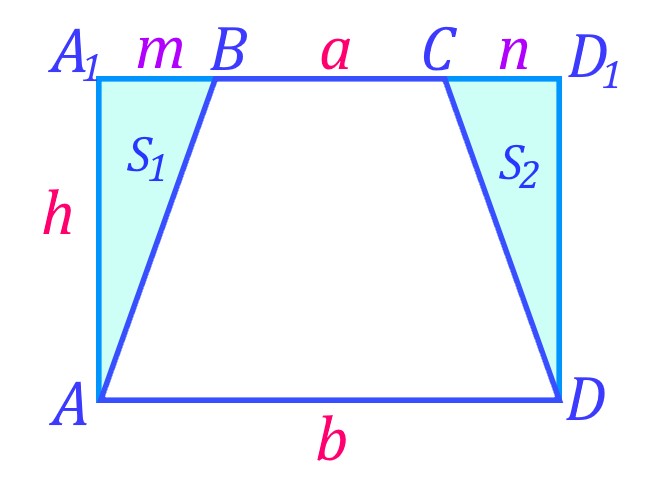
Находим ![]() .
.
Можно еще привести множество доказательств правильности формулы для площади трапеции, но двух уже достаточно.
Давайте теперь решим несколько задач на нахождение площади трапеции.
Как найти площадь равнобедренной трапеции? Точно также как и площадь любой другой трапеции. Формула одна и та же.
Примеры решения задач
Решим задачи, в которых нужно узнать площадь трапеции.
Задача 1
Вычислить площадь четырехугольника ![]() , если известно, что
, если известно, что ![]() ,
, ![]() и боковая сторона
и боковая сторона ![]() перпендикулярна к
перпендикулярна к ![]() , а
, а ![]() .
.
Решение.
По последнему условию боковая сторона ![]() является высотой трапеции.
является высотой трапеции.
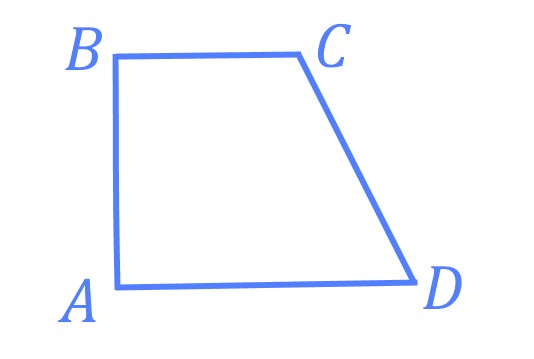
Тогда ![]() .
.
Ответ: 30.
Задача 2
Дана трапеция ![]() . Известно, что
. Известно, что ![]() см,
см, ![]() ,
, ![]() см, а ∠
см, а ∠![]() =30°. Найти
=30°. Найти ![]() .
.

Решение:
Для определения площади нам потребуется знать высоту ![]() . Определим ее из прямоугольного треугольника
. Определим ее из прямоугольного треугольника ![]() . Катет, лежащий напротив угла в 30 градусов равен половине гипотенузы, а, следовательно,
. Катет, лежащий напротив угла в 30 градусов равен половине гипотенузы, а, следовательно, ![]() см.
см.
Определим ![]() . Так как
. Так как ![]() , то получим:
, то получим: ![]() см.
см.
Тогда ![]() см.
см.
Ответ: 9 см.
Формулы площади трапеции для всех трапеций
Ниже приведем все формулы для определения площади трапеции, которые можно использовать. Однако, многие из них выводятся из основной, приведенной выше и редко используются как самостоятельные. Запоминать их нет необходимости, так как их всегда можно вывести. Однако, если вам дана задача с исходными данными и нужно проверить правильность ее решения, именно с исходными данными (например, даны только длины всех сторон трапеции, а нужно найти ее площадь), то используйте наши онлайн-калькуляторы.
По высоте и основаниям
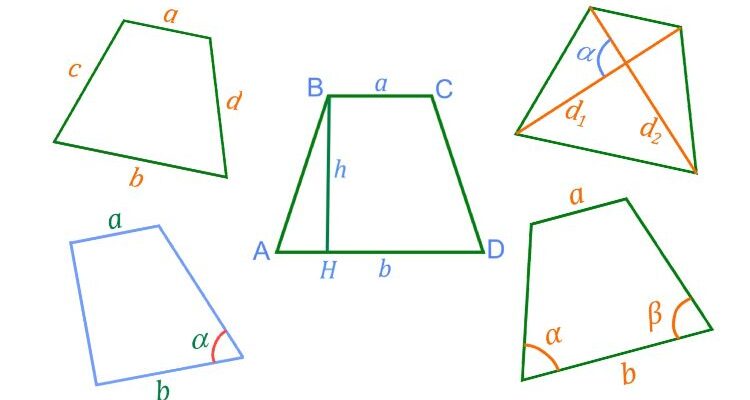
Проверьте вычисления, используя наш онлайн калькулятор. Десятичные дроби вводите через точку. Ориентируйтесь на обозначения на рисунке.
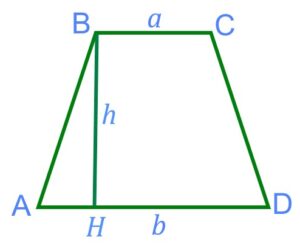
Площадь трапеции ![]()
По высоте и средней линии
Если дана высота и средняя линяя трапеции, то ее площадь можно найти по формуле:
![]()
где ![]() — средняя линия трапеции,
— средняя линия трапеции,
![]() — высота.
— высота.
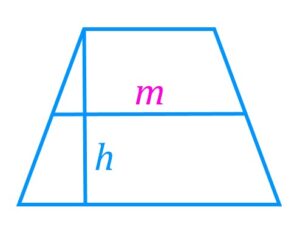
Площадь трапеции ![]()
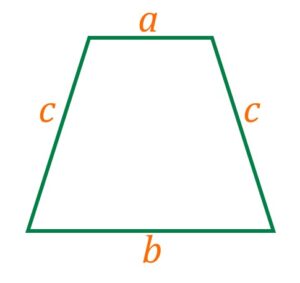
По известным четырем сторонам
Если известны стороны трапеции ![]() ,
, ![]() ,
, ![]() ,
, ![]() , то формула площади:
, то формула площади:
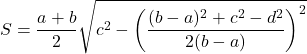
Вы можете воспользоваться онлайн калькулятором:
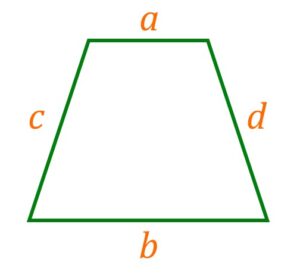
Площадь трапеции 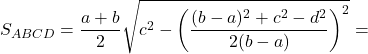
По известным основаниям и углам при основании
Если известны стороны трапеции ![]() ,
, ![]() и углы при основании, то формула площади:
и углы при основании, то формула площади:
![]()
Вы можете воспользоваться онлайн калькулятором:
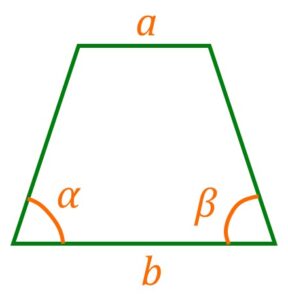
Площадь трапеции ![]()
По двум диагоналям и углу между ними
Если известны диагонали трапеции ![]() ,
, ![]() и угол
и угол ![]() между ними, то формула площади трапеции:
между ними, то формула площади трапеции:
![]()
Если вам известны эти величины, то можно быстро найти площадь, используя наш калькулятор онлайн:
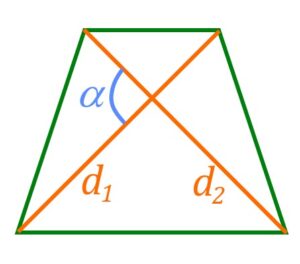
Площадь трапеции ![]()
Площадь прямоугольной трапеции
Если известны основания прямоугольной трапеции ![]() ,
, ![]() и угол
и угол ![]() у большего основания, то формула площади трапеции:
у большего основания, то формула площади трапеции:
![]()
Вывод формулы: действительно, для произвольной неравнобедренной и не прямоугольной трапеции площадь по известным основаниям и углам при основании определяется по формуле:
![]() .
.
Если угол при основании равен 90 градусов (для прямоугольной трапеции) (пусть это угол ![]() ) то
) то ![]() получим
получим
![]() .
.
По формулам приведения ![]()
Тогда формула примет вид:
![]() , так как
, так как ![]() , то окончательно получается:
, то окончательно получается:
![]()
Если вам известны эти величины, то можно быстро найти площадь, используя наш калькулятор онлайн:
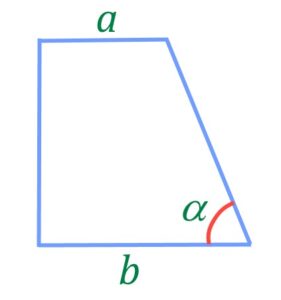
Площадь трапеции ![]()
Площадь равнобедренной трапеции
Площадь равнобедренной трапеции можно найти по любой из вышеприведенных формул, кроме формулы для прямоугольной трапеции, если ввести одинаковые значения для боковых сторон.
Например, формула нахождения площади по известным сторонам, упростится и будет иметь вид:
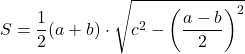
Площадь трапеции 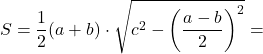
Таблица формул для определения площади трапеции
Сведем для удобства все формулы в таблицу. Если вам дана прямоугольная или равнобедренная трапеция, вы всегда можете определить ее площадь по любой из формул для неравнобедренной (произвольной) трапеции, просто введите одинаковые значения для боковой стороны.
| Известные величины для расчета | Рисунок | Формула |
| Высота и основания |  | |
| Высота и средняя линия |  | |
| Все стороны |  | 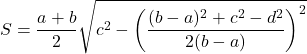 |
| Основания и углы при основании |  | |
| Две диагонали и угол между ними |  | |
| Угол при основании 90° (случай прямоугольной трапеции), известен другой угол при основании и основания |  | |
| Боковые стороны равны (случай равнобедренной трапеции), известны стороны |  | 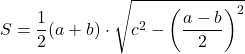 |





Класс. Спасибо.
Какая работа проведена автором! Спасибо большое, я обнаружила, что кое-что не знала раньше.
Вот это да. Сколько калькуляторов! Я в шоке просто! Спасибо. Это круто!
Много калькуляторов.