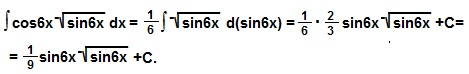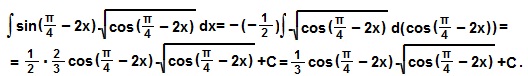11.1.8. Техника интегрирования тригонометрических функций

На предыдущем занятии (11.1.7.) мы рассмотрели простые примеры интегралов тригонометрических функций, когда подынтегральное выражение можно было упростить, используя подходящее тригонометрическое тождество, а затем применить соответствующую формулу интеграла тригонометрической функции. Кроме того, во всех примерах предыдущего занятия мы интегрировали путем подведения под знак интеграла той линейной функции, которая являлась аргументом полученной тождественными преобразованиями тригонометрической функции.

Примеры этого занятия чуть сложнее, так как подынтегральное выражение нельзя будет упростить с помощью тригонометрического тождества. А как же будем решать? Мы продолжим применять тот же метод подведения под знак дифференциала, но уже подводить под знак дифференциала будем не просто линейную функцию, а тригонометрическую функцию, зависящую от линейной функции.

Пример 1

∫sin⁷xcosxdx.

Подынтегральное выражение представляет собой произведение степени синуса на производную основания степени – синуса икс: (sinx)' = cosx.

Воспользуемся способом подведения под знак дифференциала и формулой интеграла степенной функции (формула 1) лист Интегралы). Заменяем cosxdx на d (sinx).

∫sin⁷xcosxdx =∫sin⁷xd (sinx) =(1/8) sin⁸x  + C.

Пример 2

∫sin⁷(4x + 5) cos (4x + 5) dx =(¼)∫sin⁷(4x + 5) d (sin (4x + 5)) =

=(¼)·(1/8)·sin⁸(4x+5)+C=(1/32) sin⁸(4x+5)+C.

Пример 3

∫sin3xcos⁴3xdx.  Воспользуемся способом подведения под знак дифференциала и формулой интеграла степени. Один множитель подынтегрального выражения cos⁴3x оставим, а sin3xdx запишем в виде: d (cos3x).

Проверка: d (cos3x) = — 3sin3x. Следовательно, перед знаком интеграла поставим коэффициент: — (1/3).

∫sin3xcos⁴3xdx= — (1/3)∫cos⁴3xd (cos3x) = — (1/3)·(1/5)·cos⁵3x+C = — (1/15) cos⁵3x+C.

Пример 4

Увидели формулу 4) (лист Интегралы):

В самом деле, u = sinx, du = d (sinx) = cosxdx. Тогда:

Пример 5

(такой же пример со сложным аргументом у тригонометрических функций).

А теперь пример на ту же формулу 4) (лист Интегралы), только в качестве u будет использована функция косинуса, а именно: u=cosx, отсюда du=-sinxdx.

Пример 6

Пример 7

В следующих примерах мы также будем подводить функцию под знак интеграла, а затем применять формулу 2) (лист Интегралы):

Пример 8

Пример 9

И примеры чуть сложнее:

Пример 10

Пример 11