5.3.5. Нахождение наименьшего общего кратного (НОК) данных чисел

•  Наименьшим общим кратным данных натуральных чисел называют наименьшее натуральное число, кратное каждому из данных чисел. Пример. НОК(24, 42)=168. Это самое маленькое число, которое делится и на 24 и на 42.
•  Для нахождения НОК нескольких данных натуральных чисел надо: 1) разложить каждое из данных чисел на простые множители; 2) выписать разложение большего из чисел и умножить его на недостающие множители из разложений других чисел.
•  Наименьшее кратное двух взаимно простых чисел равно произведению этих чисел.

Пример 1

Найти НОК(35; 40).

Разложим числа 35 и 40 на простые множители.

35=5∙7,   40=2∙2∙2∙5 или 40=2³∙5

Берем разложение большего числа 40 и дополняем его недостающими         множителями.  НОК(35; 40)=2³∙5∙7=40∙7=280.

Ответ: НОК(35; 40)=280.

Пример 2

Найти НОК(45; 54).

Раскладываем числа 45 и 54 на простые множители.

45=3²∙5,  54=2∙3³.

Берем разложение числа 54 и умножаем на недостающие множители из разложения числа 45, т. е. на число 5.

НОК(45; 54)=2∙3³∙5=54∙5=270.

Ответ: НОК(45; 54)=270.

Пример 3

Найти НОК(75; 120; 150).

Разложим числа 75, 120 и 150 на простые множители.

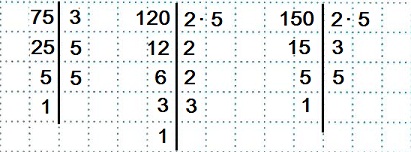75=3∙5²,    120=2³∙3∙5,  150=2∙3∙5²

Возьмем разложение большего числа 150 и дополним его двумя «двойками», так как в разложении числа 120 имеется три «двойки», а в разложении числа 150 – только одна.

НОК(75; 120; 150)=2∙3∙5²∙2∙2=150∙4=600.

Ответ: НОК(75; 120; 150)=600.

Вывод: при нахождении НОК выписывают произведение всех простых (различных) множителей, имеющихся в разложениях этих чисел, причем, каждый из множителей берется с наибольшим из имеющихся показателей степеней.