Деление и числителя и знаменателя дроби на их общий делитель, отличный от единицы, называют сокращением дроби.
Чтобы сократить обыкновенную дробь, нужно разделить ее числитель и знаменатель на одно и то же натуральное число.
Это число является наибольшим общим делителем числителя и знаменателя данной дроби.
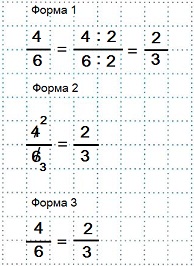
Возможны следующие формы записи решения примеров на сокращение обыкновенных дробей.
Учащийся вправе выбрать любую форму записи.
Примеры. Упростить дроби.
Содержание
Пример 1
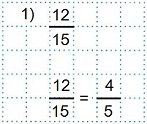Сократим дробь на 3 (делим числитель на 3;
делим знаменатель на 3).
Пример 2
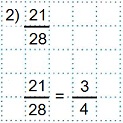Сокращаем дробь на 7.
Пример 3
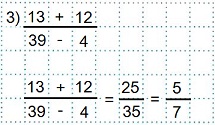Выполняем указанные действия в числителе и знаменателе дроби.
Полученную дробь сокращаем на 5.
Пример 4
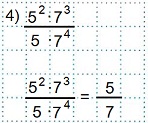Сократим данную дробь 4) на 5·7³ — наибольший общий делитель (НОД) числителя и знаменателя, который состоит из общих множителей числителя и знаменателя, взятых в степени с наименьшим показателем.
Пример 5
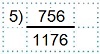Разложим числитель и знаменатель этой дроби на простые множители.
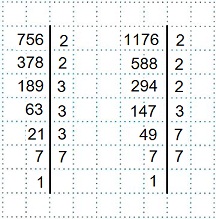Получаем: 756=2²·3³·7 и 1176=2³·3·7².
Определяем НОД (наибольший общий делитель) числителя и знаменателя дроби 5).
Это произведение общих множителей, взятых с наименьшими показателями.
НОД(756; 1176)=2²·3·7.
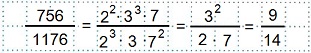Делим числитель и знаменатель данной дроби на их НОД, т. е. на 2²·3·7 получаем несократимую дробь 9/14.
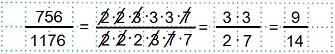А можно было записать разложения числителя и знаменателя в виде произведения простых множителей, не применяя понятие степени, а затем произвести сокращение дроби, зачеркивая одинаковые множители в числителе и знаменателе. Когда одинаковых множителей не останется — перемножаем оставшиеся множители отдельно в числителе и отдельно в знаменателе и выписываем получившуюся дробь 9/14.
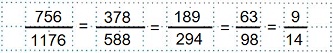И, наконец, можно было сокращать данную дробь 5) постепенно, применяя признаки деления чисел и к числителю и к знаменателю дроби. Рассуждаем так: числа 756 и 1176 оканчиваются четной цифрой, значит, оба делятся на 2. Сокращаем дробь на 2. Числитель и знаменатель новой дроби — числа 378 и 588 также делятся на 2. Сокращаем дробь на 2. Замечаем, что число 294 — четное, а 189 — нечетное, и сокращение на 2 уже невозможно. Проверим признак делимости чисел 189 и 294 на 3.
(1+8+9)=18 делится на 3 и (2+9+4)=15 делится на 3, следовательно, и сами числа 189 и 294 делятся на 3. Сокращаем дробь на 3. Далее, 63 делится на 3, а 98 — нет. Перебираем другие простые множители. Оба числа делятся на 7. Сокращаем дробь на 7 и получаем несократимую дробь 9/14.
