Одинаковые знаменатели
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше, и меньше та, у которой числитель меньше. На самом деле, ведь знаменатель показывает, на сколько частей разделили одну целую величину, а числитель показывает, сколько таких частей взяли.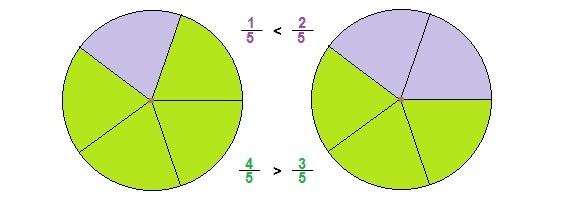
Получается, что делили каждый целый круг на одно и то же число 5, а брали разное количество частей: больше взяли — большая дробь и получилась.
Одинаковые числители
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше, и меньше та, у которой знаменатель больше. Ну и, в самом деле, если мы один круг разделим на 8 частей, а другой на 5 частей и возьмем по одной части от каждого из кругов. Какая часть будет больше?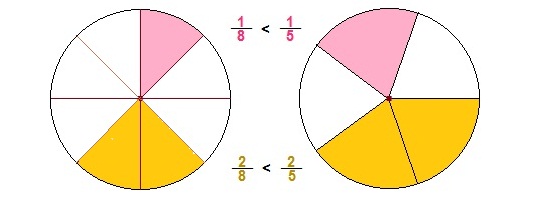
Конечно, от круга, поделенного на 5 частей! А теперь представьте, что делили не круги, а торты. Вы бы какой кусочек предпочли, точнее, какую долю: пятую или восьмую?
Разные числители и знаменатели
Чтобы сравнить дроби с разными числителями и разными знаменателями, надо привести дроби к наименьшему общему знаменателю, а затем сравнивать дроби с одинаковыми знаменателями.
Примеры. Сравнить обыкновенные дроби:
![]()
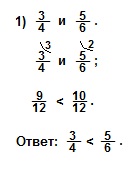 Приведем эти дроби к наименьшему общему знаменателю. НОЗ(4; 6)=12. Находим дополнительные множители для каждой из дробей. Для 1-й дроби дополнительный множитель 3 (12:4=3). Для 2-й дроби дополнительный множитель 2 (12:6=2). Теперь сравниваем числители двух получившихся дробей с одинаковыми знаменателями. Так как числитель первой дроби меньше числителя второй дроби (9 < 10), то и сама первая дробь меньше второй дроби.
Приведем эти дроби к наименьшему общему знаменателю. НОЗ(4; 6)=12. Находим дополнительные множители для каждой из дробей. Для 1-й дроби дополнительный множитель 3 (12:4=3). Для 2-й дроби дополнительный множитель 2 (12:6=2). Теперь сравниваем числители двух получившихся дробей с одинаковыми знаменателями. Так как числитель первой дроби меньше числителя второй дроби (9 < 10), то и сама первая дробь меньше второй дроби.
Аналогично рассуждаем и при решении остальных примеров.
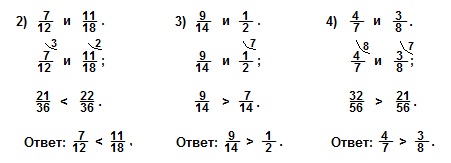









That's raelly shrewd! Good to see the logic set out so well.
Fianlly! This is just what I was looking for.
Выглядит убедительно) когда-то в школе дроби давались с трудом, но здесь все объяснено очень доходчиво. Автор статьи молодец!