5.6.3. Решение задач на проценты. Часть В

Задача 1

Первое число составляет 80% от второго. А сколько процентов второе число составляет от первого?

Решение. Обозначим второе число через х. Тогда первое число по равно 0,8х. Найдем, сколько второе число составляет от первого. Для этого разделим второе число на первое, и результат умножим на 100%.

Ответ: второе число составляет 125% от первого.

Задача 2

На сколько процентов увеличится площадь квадрата, если его сторону увеличить на 30%?

Решение. Если сторона квадрата равна а, то площадь квадрата S=а². После увеличения стороны на 30% ее длина составит 130% от а. Это 1,3а. Новая площадь S₁=(1,3a)²=1,69a². Разница составила 0,69а². Обращаем десятичную дробь 0,69 в проценты и получаем 69%. Ответ: Если сторону квадрата увеличить на 30%, то площадь квадрата увеличится на 69%.

Задача 3

Яблоки, содержащие 70% воды, потеряли при сушке 60% своей массы. Сколько процентов воды содержат сушеные яблоки?

Решение. Пусть было х яблок по массе. В них содержится 70% воды, значит, 30% сухого концентрата. 30% от х – это 0,3х. После сушки яблок это количество 0,3х сухого вещества так и остается. Известно, что при сушке яблоки потеряли 60% своей массы. Следовательно, осталось 40% от х, Это 0,4х. То, что осталось, примем за 100%. В этой массе 0,3х сухого вещества. Узнаем, сколько это процентов.

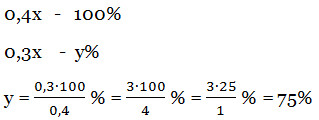
В сушеных яблоках 75% сухого вещества, значит, воды в сушеных яблоках 100%-75%=25%. Ответ: в сушеных яблоках 25% воды.

Задача 4

Свежие грибы содержат 90% влаги, сушеные – 12%. Сколько сушеных грибов получится из 13,2 кг свежих?

Решение. Пусть из 13,2 кг свежих грибов получится х кг сушеных грибов. Тогда сухого вещества в х кг будет содержаться 100%-12%=88%. Получается 0,88х кг. В 13,2 кг свежих грибов сухого вещества содержится 100%-90%=10%. В килограммах получается 0,1∙13,2=1,32 кг. Имеем равенство: 0,88х=1,32, отсюда х=1,32 : 0,88;

х=1,5 кг. Ответ: из 13,2 кг свежих грибов получается 1,5 кг сушеных грибов.

Задача 5

Сколько литров воды нужно разбавить с 300 г соли для получения раствора с концентрацией 15%?

Решение. Пусть нужно х граммов воды разбавить с 300 г соли для получения раствора с концентрацией 15%. Выразим количество соли в х г воды 15%-го раствора. Это 15% от х. Получаем 0,15х г. По условию соли 300 г. Получаем равенство:

0,15х=300, отсюда х=300:0,15=30000:15=2000 г = 2 л воды.

Ответ: нужно разбавить 2 л воды.

Задача 6

В раствор сахарной воды массой 200 г с концентрацией 30% налили 100 г чистой воды. Сколько процентов составляет концентрация сахара в последнем растворе?

Решение. В 200 г сахарной воды с концентрацией 30% содержится 0,3∙200=60 г сахара. После того, как в раствор налили 100 г чистой воды, масса раствора стала равной 300 г, а сахара в нем по-прежнему 60 г. Найдем процентное отношение массы сахара к массе раствора.

Ответ: концентрация сахара в последнем растворе составляет 20%.

Задача 7

В раствор соленой воды массой 600 г с концентрацией 15% добавили раствор соленой воды массой 240 г с концентрацией 50%. Сколько процентов соли в полученной смеси?

Решение. В 600 г соленой воды с концентрацией 15% содержится 15% от 600 г соли. Это 0,15∙600=90 г соли. В 240 г соленой воды с концентрацией 50% содержится 50% от 240 г соли. Это 0,5∙240=120 г соли. Масса полученной смеси равна 600+240=840 г. Соли в этой массе 90+120=210 г. Найдем процент соли в полученной смеси.

Ответ: в полученной смеси содержится 25% соли.

Задача 8

Цену товара сначала снизили на 20%, затем новую цену снизили еще на 25%. На сколько процентов снизили первоначальную цену товара?

Решение. Обозначив первоначальную стоимость товара через х, выразим окончательную стоимость товара и найдем, сколько процентов последняя цена товара будет составлять от первоначальной. После первого снижения на 20%  товар стал стоить 80% от первоначальной цены. Это 80% от х или 0,8х Эту цену снизили еще на 25%, стоимость стала составлять 75% от последней цены, равной 0,8х. Тогда последняя цена составит 75% от 0,8х или 0,75∙0,8х=0,6х. Находим, сколько процентов 0,6х (последняя цена товара) составляет от х (первоначальной цены товара).

Получается, что новая цена составляет 60% от первоначальной цены. Это означает, что цена товара после двух снижений уменьшилась на 40%. Ответ: цену товара снизили на 40%.

Задача 9

Число увеличили на 25%. На сколько процентов нужно уменьшить полученное число, чтобы вновь получилось заданное?

Решение. Пусть заданное число было равно х. После увеличения оно составит 1,25х (это 125% от х). Выясним, сколько процентов от  числа 1,25х нужно взять, чтобы опять получить х. Получается, что:

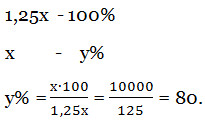
Так как х составляет от 1,25х только 80%, то это означает, что, для того, чтобы получить заданное число, нужно полученное число уменьшить на 100%-80%=20%.   Ответ: на 20%.

Если вы хотите научиться решать задачи на проценты, то полезной будет также и эта ссылка: перейдите по ссылке.