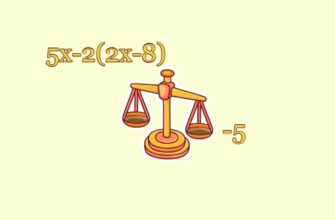Найдите значение выражения (16 \cdot 10^{-2})^2 \cdot (13 \cdot 10^4)
Решение:
При возведении в степень показатели степени перемножаются. Это свойство степени: (a^m)^n=a^{mn}.
А также при возведении в степень произведения мы должны возвести в степень каждый множитель: (a^m \cdot b^n)^k=a^{mk} \cdot b^{nk}.
Тогда выражение запишется так:
(16 \cdot 10^{-2})^2 \cdot (13 \cdot 10^4)=16^2 \cdot 10^{-2 \cdot (-2)} \cdot 13 \cdot 10^4=16^2 \cdot 10^{-4} \cdot 13 \cdot 10^4
Так как 10^{-4} \cdot 10^4=10^{-4+4}=10^0=1
Таким образом получаем:
(16 \cdot 10^{-2})^2 \cdot (13 \cdot 10^4)=16^2 \cdot 13 \cdot 1=3328
Ответ: 3328
Похожее задание: Найдите значение выражения (2*10^2)^4*(19*10^-6)