Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь. Давайте рассмотрим это свойство дроби подробнее. Нарисуем круг и разделим его на 4 части. Обратим внимание, что если мы возьмем три таких части это будет все равно, если мы нарисуем круг, разделим его на 8 частей и возьмем 6 таких частей, или разделим круг на 12 частей и возьмем 9 таких частей.
Содержание
Доказательство основного свойства дроби
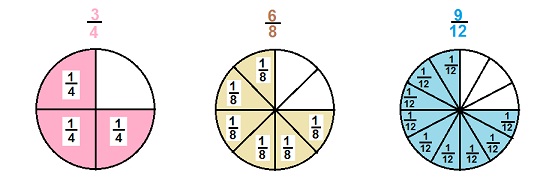
Закрашенные области всех трех кругов равны между собой, но над кругами записаны различные обыкновенные дроби. Почему? И все ли верно? Да, все верно, ведь можно разделить круг на:
- 4 части и закрасить 3 такие части;
- 8 частей и закрасить 6 таких частей;
- 12 частей и закрасить 9 таких частей.
Следовательно,
Мы убедились в правильности высказывания: если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Рассмотрим несколько примеров на основное свойство дроби.
Пример 1
Используя основное свойство дроби, замените звездочку таким числом, чтобы равенство было верным.
Рассуждаем так: числитель нужно увеличить во столько же раз, во сколько увеличили знаменатель дроби, т. е. в 4 раза (16:4=4). Вместо звездочки запишем значение 3·4=12.
Пример 2
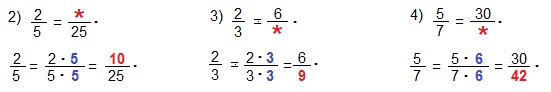
Пример 3
Рассуждаем так: знаменатель нужно уменьшить во столько же раз, во сколько уменьшили числитель дроби, т. е. в 7 раз (21:3=7). Вместо звездочки запишем значение 28:7=4.
Пример 4
Итак, зная основное свойство дроби, можно с успехом преобразовывать обыкновенные дроби, определять знаменатель или числитель в равной дроби.
