Содержание
Тезис I
Множество представляет собой совокупность некоторых предметов или чисел, составленных по каким-либо общим свойствам или законам (множество букв на странице, множество правильных дробей со знаменателем 5, множество звезд на небе и т.д.).
Для записи множества используют фигурные скобки: «{ »- множество открывается; "}" — множество закрывается. А само множество называют заглавными латинскими буквами: А, В, С и так далее.
Примеры.
1. Записать множество А, состоящее из всех гласных букв в слове «математика».
Решение. А={а, е, и}. Вы видите: несмотря на то,что в слове «математика» имеется три буквы «а» — в записи множества повторений не допускается, и буква «а» записывается только один раз. Множество А состоит из трех элементов.
2. Записать множество всех правильных дробей со знаменателем 5.
Решение. Вспоминаем: правильной называют обыкновенную дробь, у которой числитель меньше знаменателя. Обозначим через В искомое множество. Тогда:
Множество В состоит из четырех элементов.
Тезис II
Множества состоят из элементов и бывают конечными или бесконечными. Множество, которое не содержит ни одного элемента, называют пустым множеством и обозначают Ø.
Тезис III
Множество В называют подмножеством множества А, если все элементы множества В являются элементами множества А.
3. Какое из двух данных множеств В и С является подмножеством множества К,
если В={-1; 3; 4}, C={0; 3; 4; 5), K={0; 2; 3; 4; 5; 6} ?
Решение. Все элементы множества С являются также элементами множества К, поэтому, множество С является подмножеством множества К. Записывают:
Тезис IV
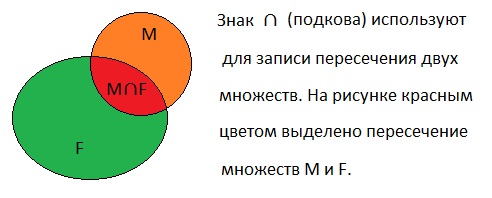
Пересечением множеств А и В называется множество, элементы которого принадлежат и множеству А и множеству В.
4. Показать пересечение двух множеств М и F с помощью кругов Эйлера.
Решение.
Тезис V
Объединением множеств А и В называется множество, элементы которого принадлежат хотя бы одному из данных множеств А и В.
5. Показать с помощью кругов Эйлера объединение множеств Т и Р.
Решение.
