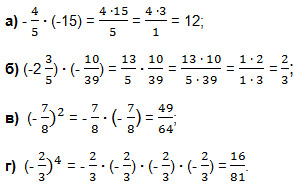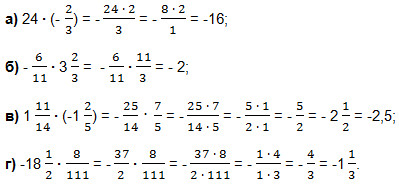Содержание
Умножение отрицательных чисел
Произведение двух отрицательных чисел есть число положительное. Модуль произведения равен произведению модулей данных чисел.
Так как произведение положительных чисел — это тоже положительное число, то сделаем ВЫВОД:
Произведение двух чисел с одинаковыми знаками есть число положительное. Модуль этого числа равен произведению модулей данных чисел.
Пример 1
Выполните умножение (устно):
а) -12·(-10); б) -0,05·(-100); в) -3,5·(-2); г) -0,12·(-0,5).
Решение. При решении всех примеров пользуемся правилом произведения двух отрицательных чисел. При решением примеров а) и б) применяем правило умножения десятичной дроби на 10, 100, 1000 и т.д. При решении примеров в) и г) применим правило умножения десятичной дроби на десятичную дробь. Если забыли, как это делается - смотрите здесь!
а) -12·(-10)=120; б) -0,05·(-100)=5; в) -3,5·(-2)=7; г) -0,12·(-0,5)=0,06.
Пример 2
Вычислить:
Решение. Смешанное число в примере б) обратим в неправильную дробь. В примере в) вторую степень дроби заменим произведением двух одинаковых дробей. В примере г) четвертую степень дроби представим в виде произведения четырех одинаковых множителей.
Умножение чисел с разными знаками
Произведение двух чисел с разными знаками есть число отрицательное. Модуль произведения равен произведению модулей данных чисел.
Пример 3
Вычислить устно:
а) -10·0,35; б) 4,1·(-100); в) 2,5·(-0,4); г) -0,05·200.
Решение. Применяем правило умножения двух чисел с разными знаками. Перемножим модули множителей и перед результатом поставим знак «минус».
а) -10·0,35=-3,5; б) 4,1·(-100)=-410; в) 2,5·(-0,4)=-1; г) -0,05·200=-10.
Пример 4
Вычислить:
Решение.
ЗАПОМНИЛИ:
Произведение двух чисел с одинаковыми знаками есть число положительное.
Произведение двух чисел с разными знаками есть число отрицательное.