- Две взаимно перпендикулярные координатные прямые, пересекающиеся в точке О — начале отсчета, образуют прямоугольную систему координат, называемую также декартовой системой координат.
- Плоскость, на которой выбрана система координат, называется координатной плоскостью. Координатные прямые называются координатными осями. Горизонтальная — ось абсцисс (Ох), вертикальная — ось ординат (Оy).
- Координатные оси разбивают координатную плоскость на четыре части — четверти. Порядковые номера четвертей принято считать против часовой стрелки.
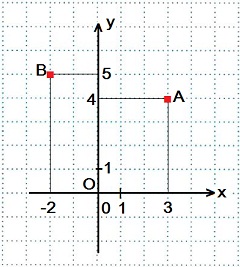
- Любая точка в координатной плоскости задается своими координатами - абсциссой и ординатой. Например, А(3; 4). Читают: точка А с координатами 3 и 4. Здесь 3 — абсцисса, 4 — ордината.
I. Построение точки А(3; 4).
Абсцисса 3 показывает, что от начала отсчета — точки О нужно отложить вправо 3 единичных отрезка, а затем вверх отложим 4 единичных отрезка и поставим точку.
Это и есть точка А(3; 4).
Построение точки В(-2; 5).
От нуля отложим влево 2 единичных отрезка, а затем вверх 5 единичных отрезков.
Ставим точку В.
Обычно за единичный отрезок принимают 1 клетку.
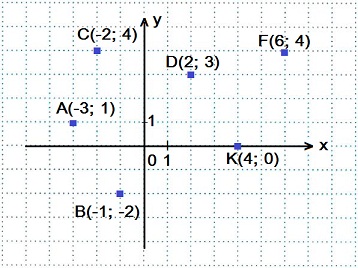II. В координатной плоскости xOy построить точки:
A (-3; 1); B (-1; -2);
C (-2: 4); D (2; 3);
F (6: 4); K (4; 0)
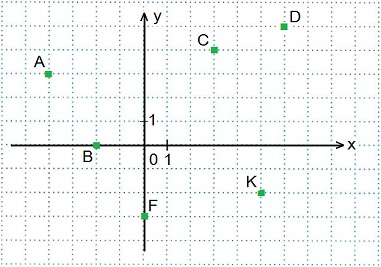
III. Определить координаты построенных точек: A, B, C, D, F, K.
Ответы.
А(-4; 3); В(-2; 0);
С(3; 4); D (6; 5);
F (0; -3); K (5; -2).
