- Две точки А и А1 называются симметричными друг другу относительно прямой m, если прямая m перпендикулярна отрезку АА1 и проходит через его середину. Прямую m называют осью симметрии.
- При сгибании плоскости чертежа по прямой m – оси симметрии симметричные фигуры совместятся.
- Прямоугольник имеет две оси симметрии.
- Квадрат имеет четыре оси симметрии.
- Любая прямая, проходящая через центр окружности, является ее осью симметрии. Окружность имеет бесконечное множество осей симметрии.
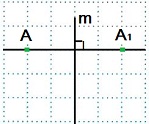Точки А и А1 симметричны относительно прямой m, так как прямая m перпендикулярна отрезку АА1 и проходит через его середину.
m – ось симметрии.
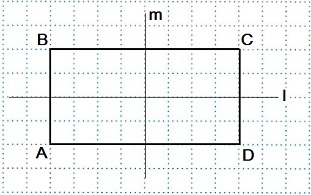Прямоугольник ABCD имеет две оси симметрии: прямые m и l.
Если чертеж перегнуть по прямой m или по прямой l, то обе части чертежа совпадут.
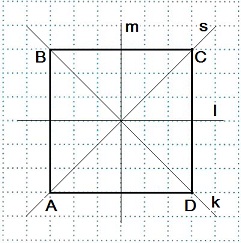Квадрат ABCD имеет четыре оси симметрии: прямые m, l, k и s.
Если квадрат перегнуть по какой-либо из прямых: m, l, k или s, то обе части квадрата совпадут.
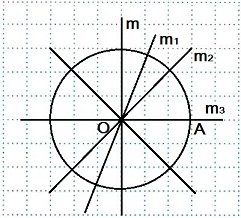Окружность с центром в точке О и радиусом ОА имеет бесчисленное количество осей симметрии. Это прямые: m, m1, m2, m3 ...
Задание. Построить точку А1, симметричную точке А(-4; 2) относительно оси Ох.
Построить точку А2, симметричную точке А(-4; 2) относительно оси Оy.
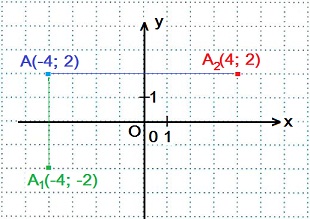Точка А1(-4; -2) симметрична точке А(-4; 2) относительно оси Ох, так как ось Ох перпендикулярна отрезку АА1 и проходит через его середину.
У точек, симметричных относительно оси Ох абсциссы совпадают, а ординаты являются противоположными числами.
Точка А2(4; -2) симметрична точке А(-4; 2) относительно оси Оy, так как ось Оу перпендикулярна отрезку АА2 и проходит через его середину.
У точек, симметричных относительно оси Оу ординаты совпадают, а абсциссы являются противоположными числами.
