Чтобы решить систему линейных уравнений с двумя переменными методом сложения, надо:
1) умножить левую и правую части одного или обоих уравнений на некоторое число так, чтобы коэффициенты при одной из переменных в уравнениях стали противоположными числами;
2) сложить почленно полученные уравнения и найти значение одной из переменных;
3) подставить найденное значение одной переменной в одно из данных уравнений и найти значение второй переменной.
Если в данной системе коэффициенты при одной переменной являются противоположными числами, то решение системы начнём сразу с пункта 2).
Примеры. Решить систему линейных уравнений с двумя переменными методом сложения.
Пример 1
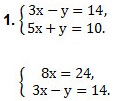
Так как коэффициенты при у являются противоположными числами (-1 и 1), то решение начинаем с пункта 2). Складываем уравнения почленно и получим уравнение 8х = 24. Вторым уравнением системы можно записать любое уравнение исходной системы.
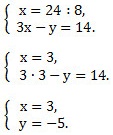 Найдём х и подставим его значение во 2-ое уравнение.
Найдём х и подставим его значение во 2-ое уравнение.
Решаем 2–ое уравнение: 9-у = 14, отсюда у = -5.
Сделаем проверку. Подставим значения х = 3 и у = -5 в первоначальную систему уравнений.
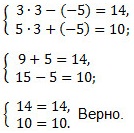 Примечание. Проверку можно сделать устно и не записывать, если наличие проверки не оговорено в условии.
Примечание. Проверку можно сделать устно и не записывать, если наличие проверки не оговорено в условии.
Ответ: (3; -5).
Пример 2
![]() Если мы умножим 1-ое уравнение на (-2), то коэффициенты при переменной х станут противоположными числами:
Если мы умножим 1-ое уравнение на (-2), то коэффициенты при переменной х станут противоположными числами:
![]() Сложим эти равенства почленно.
Сложим эти равенства почленно.
Мы получим равносильную систему уравнений, в которой 1-ое уравнение есть сумма двух уравнений прежней системы, а 2-м уравнением системы мы запишем 1-ое уравнение исходной системы (обычно записывают уравнение с меньшими коэффициентами):
![]() Находим у из 1-го уравнения и полученное значение подставляем во 2-ое.
Находим у из 1-го уравнения и полученное значение подставляем во 2-ое.
Решаем последнее уравнение системы и получаем х = -2.
Ответ: (-2; 1).
Пример 3
![]() Сделаем коэффициенты при переменной у противоположными числами. Для этого все члены 1-го уравнения умножим на 5, а все члены 2-го уравнения на 2.
Сделаем коэффициенты при переменной у противоположными числами. Для этого все члены 1-го уравнения умножим на 5, а все члены 2-го уравнения на 2.
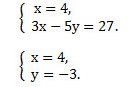 Подставим значение х=4 во 2-ое уравнение.
Подставим значение х=4 во 2-ое уравнение.
3 · 4 — 5у = 27. Упростим: 12 — 5у = 27, отсюда -5у = 15, а у = -3.
Ответ: (4; -3).

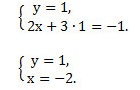







Класс👍🏻
2х+3у=5
Х-4у=1
Метод сложения
Система линейного уравнения