I. Определение. (- n)-й степенью (n – натуральное) числа а, не равного нулю, считается число, обратное n-й степени числа а:
Примеры. Вычислить:
Решение.
II. Следующая формула позволяет заменить обыкновенную дробь с отрицательным показателем на обратную ей дробь с положительным показателем:
Примеры. Вычислить:
Решение.
Свойства степени с натуральным показателем справедливы и для степеней с любым показателем.
Свойства степени с натуральным показателем с примерами смотрите в предыдущем уроке здесь.
Примеры на все свойства степени.
Упростить:
Решение.
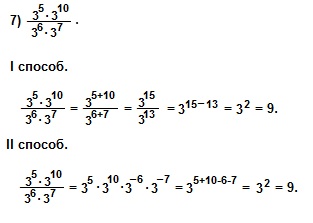 При решении 7) примера I способом мы использовали свойства умножения и деления степеней с одинаковыми основаниями: am∙an=am+n и am:an=am-n. При решении II способом мы использовали понятие степени с отрицательным показателем:
При решении 7) примера I способом мы использовали свойства умножения и деления степеней с одинаковыми основаниями: am∙an=am+n и am:an=am-n. При решении II способом мы использовали понятие степени с отрицательным показателем: ![]() и свойство произведения степеней с одинаковыми основаниями: am∙an=am+n .
и свойство произведения степеней с одинаковыми основаниями: am∙an=am+n .
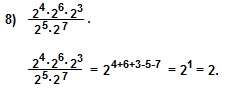 Пример 8 ) решаем так же, как решали пример 7) вторым способом.
Пример 8 ) решаем так же, как решали пример 7) вторым способом.
В примере 9) представим 73 как 72∙7, а степень 45 как 43∙42, а затем сократим дробь на (72∙43).
В 10) примере применим формулу степени произведения: (ab)n=an∙bn, а затем сократим дробь на (26∙35).

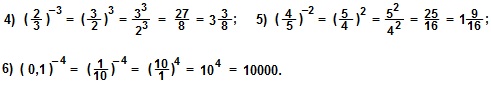
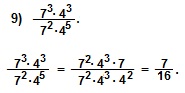
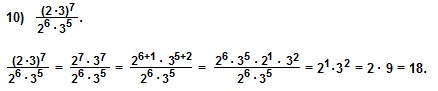





I'm ipmresesd. You've really raised the bar with that.