Рассмотрим что такое числовое неравенство, числовые неравенства имеют следующие свойства.
Свойства числовых неравенств
- Если при сравнении чисел a и b разность a-b – положительное число, то a > b.
- Если при сравнении чисел a и b разность a-b – отрицательное число, то a < b.
Строгие и нестрогие числовые неравенства:
- Если неравенства записываются знаками < или > , то их называют строгими неравенствами.
- Если неравенства записывают знаками ≤ или ≥, то их называют нестрогими неравенствами.
Как решать числовое неравенство
Примеры.
1. Сравните числа а и b по их разности.
а) a-b=-7. Решение. Так как разность a-b – отрицательное число, то a < b.
б) a-b=4,5. Решение. Так как разность a-b – положительное число, то a > b.
в) a-b=0. Решение. Так как разность a-b равна нулю, то a=b.
2. Сравните данные числа.
а) 0,099 и 0,1. Решение. Десятичные дроби сравниваются поразрядно: из двух чисел больше то, которое содержит больше единиц высшего разряда.
0,099 < 0,1, так как 0 < 1 (сравнили десятые доли чисел).
б) -5,43 и -5,6. Решение. -5,43 > -5,6, так как из двух отрицательных чисел больше то, модуль которого меньше.
так как из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, а меньше та, числитель которой меньше.

так как из двух дробей с одинаковыми числителями больше та, знаменатель которой меньше, а меньше та, знаменатель которой больше.
Решение. Приведем дроби к общему знаменателю. Получаем:
Теперь сравниваем дроби с одинаковыми знаменателями. Получаем:
3. Записать в виде двойного неравенства: 6 < 12 и 12 < 15.
Решение. 6 < 12 < 15. Читают: двенадцать больше шести и меньше пятнадцати.
4. Выписать все целые числа, удовлетворяющие двойному неравенству:
— 4 ≤ х < 3. Решение: -4; -3; -2; -1; 0; 1; 2.
5. Задания для самостоятельного решения.
5.1 Сравните с нулем разность чисел а и b, если
а) a < b; б) a > b; в) a=b.
5.2. Сравните данные числа.
а) -2,467 и -2,476; б) 8,98 и 8,899;
5.3. Выписать все целые числа, удовлетворяющие двойному неравенству:
а) -5 ≤ х < 1; б) -3 < x ≤ 3; в) 4 < x < 9; г) -8 ≤ x ≤ -4.
Ответы на решение числовых неравенств
5.1.а. a-b < 0;
5.1.б. a-b > 0;
5.1.в. a-b=0.
5.2.а. -2,467 > -2,476;
5.2.б. 8,98 > 8,899;
5.3.а -5; -4; -3; -2; -1; 0;
5.3.б. -2; -1; 0; 1; 2; 3;
5.3.в. 5; 6; 7; 8;
5.3.г. -8; -7; -6; -5; -4.


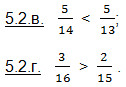





Нра