Площадь прямоугольника

Площадь прямоугольника очень часто требуется найти в задачах по геометрии. И не только — в повседневной жизни очень многие плоскости имеют форму прямоугольника и надо найти площадь прямоугольника. Как это сделать? Давайте рассмотрим все формулы и примеры.

Мы учимся вычислять площадь прямоугольника или площадь прямоугольника в школе. Однако, когда вы станете старше, вполне возможно, что вы не будете помнить, как найти площадь прямоугольника. Для начала давайте вспомним, что такое прямоугольник.

Что такое прямоугольник

Давайте не будем «срезать углы». Чтобы иметь возможность вычислить площадь прямоугольника, естественно, что мы сначала знаем, что это такое. Поэтому для начала необходимо помнить, что прямоугольник является четырехугольником. Другими словами, это геометрическая фигура, которая имеет четыре стороны и четыре прямых угла. Противоположные стороны прямоугольника имеют одинаковую длину. Две самые длинные стороны представляют его длину, а две другие стороны представляют его ширину.

Не все четырехугольники являются прямоугольниками. Действительно, обязательно, чтобы они имели следующие свойства, чтобы мы могли сказать, что это действительно прямоугольник:

Характеристики прямоугольника

Противоположные стороны должны быть параллельны.

• Диагонали прямоугольника должны быть одинаковой длины. Они также пересекаются в своей середине.
• Точка пересечения диагоналей прямоугольника называется центром симметрии.
• Кроме того, прямоугольник также является параллелограммом, так как его стороны попарно параллельны. Однако это частный случай параллелограмма. На самом деле он имеет четыре прямых угла, и его две параллельные стороны не должны иметь одинаковую длину. В противном случае все четыре стороны имеют одинаковую длину — тогда мы говорим о квадрате.

Формула площади прямоугольника

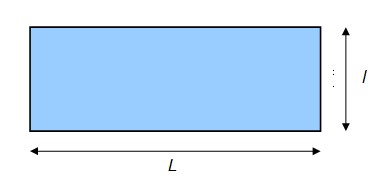
Как рассчитать площадь прямоугольника? Обратите внимание, что базовую формулу для вычисления площади (или площади) прямоугольника очень легко запомнить. Вы просто должны умножить его длину на ширину.

Например, площадь прямоугольника длиной 4 сантиметра и шириной 2 сантиметра равна 4 x 2 = 8 см².

Принцип расчета площади прямоугольника

Чтобы вычислить площадь прямоугольника, мы посчитаем количество единиц областей, которые содержит прямоугольник:

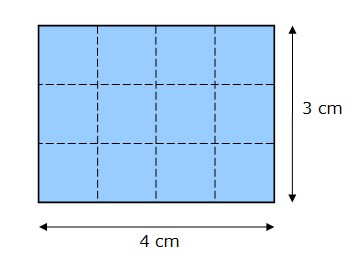
В прямоугольнике выше 12 квадратов по 1 см². Его площадь составляет 12 см² (4 х 3).

Примечание. В этом расчете длина L и ширина l прямоугольника должны быть выражены в одной и той же единице длины. Результат будет выражен в той же единице измерения, возведенной в квадрат. Например, если длина прямоугольника выражена в метрах, ширина также должна быть выражена в метрах, а результат формулы для расчета площади прямоугольника даст результат в квадратных метрах (м²).

Площадь прямоугольника эквивалентна его территории. Территория — это термин, используемый для обозначения меры площади земли (мы используем единицу измерения гектар, а не м²). Гектар — это метрическая мера земельной площади, равная 10 000 м².

Пример расчета

Рассмотрим прямоугольник длиной L = 4 см и шириной l = 2 см. Площадь S его поверхности равна:

A = L x l = 4 x 2 = 8 см².

Как рассчитать площадь прямоугольника, если мы знаем только одну сторону и диагональ

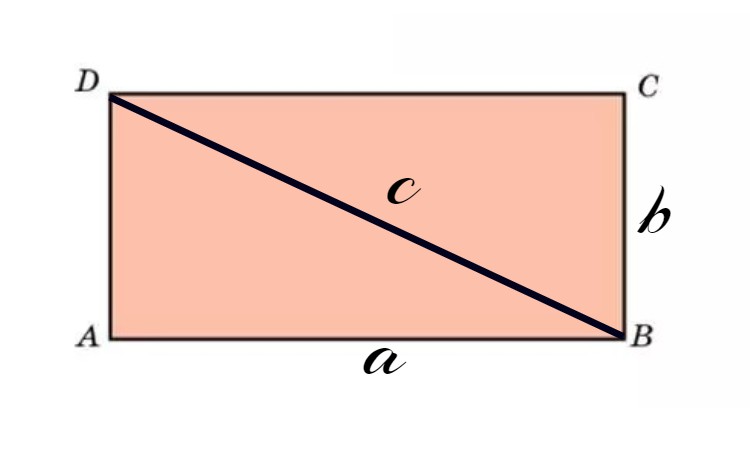
Можно определить площадь прямоугольника другим способом. Формула, которая была изложена ранее, не является единственным методом, который можно использовать. Действительно, вполне возможно сделать это по-другому. Для этого нам нужно будет, по крайней мере, измерить только одну сторону и необходимо знать длину диагонали. В этом случае мы делаем расчет, используя теорему Пифагора.

Что такое теорема Пифагора

Это формула, которая используется для определения длины третьей стороны прямоугольного треугольника, когда вы уже знаете значение двух других его сторон.

Обратите внимание, что прямоугольник состоит из двух прямоугольных треугольников. Действительно, диагональ представляет гипотенузу этого типа треугольника.

Кроме того, это также самая длинная сторона, которую можно найти на рисунке. Длина и ширина, с другой стороны, представляют две другие его стороны (скажем, смежные стороны). Это причина, почему можно использовать эту формулу для определения площади прямоугольника.

Теорема Пифагора основана на довольно простом уравнении, которое выглядит следующим образом: a² + b² = c². Где a и b используются для представления двух соседних сторон — катетов прямоугольного треугольника, а c представляет гипотенузу треугольника.

Чтобы полностью понять использование этой формулы, мы начнем с очень конкретного примера. Для этого предположим, что диагональ прямоугольника 10 см, а другая сторона 6 см. Если мы ссылаемся на формулу a² + b² = c², следовательно, сторона «a» составляет 6 см, а гипотенуза «c» — 10 см. Теперь нам нужно просто заменить буквенные значения числовыми значениями, которые у нас есть. Что дает нам:

a² + b² = c²

6² + b² = 10²

b² = 10² — 6²

b² = 100 — 36

b² = 64

b= 8

Мы получаем длину смежной стороны прямоугольника «b», которая равна 8 см. Теперь мы можем рассчитать площадь прямоугольника:

S = 8 см х 6 см

Следовательно, S = 48 см².