На рисунке изображен график y=f (x). На оси абсцисс отмечены точки -2, -1, 1, 2. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
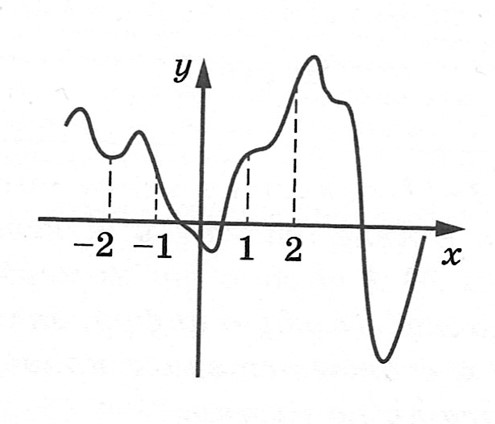
Решение:
Производная функции в точке равна тангенсу угла касательной, проведенной к графику функции в этой точке, который она образует с положительным направлением оси Ox. Тангенс угла можно затем легко найти, используя тригонометрический круг. При этом стоит учесть, что тангенс острого угла положителен, а тангенс тупого угла — отрицателен. Итак, давайте проведем касательные к графику функции в указанных точках.
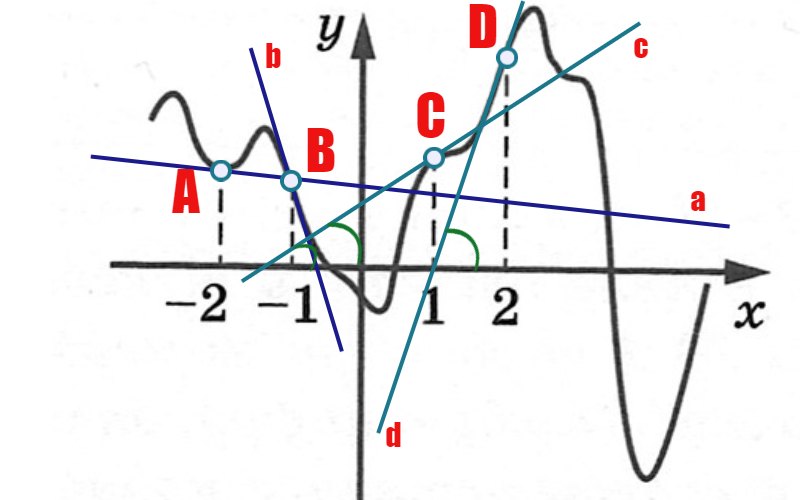
Итак, мы обозначили данные нам точки — A, B, C, D. И провели к ним касательные соответственно a, b, c, d.
Мы получаем 4 угла. Из который 2 острых угла и два тупых. В точках С и D касательные c и d составляют с положительным направлением оси Ox острый угол, а, значит, тангенсы этих углов будут положительными. То есть мы имеем два острых угла, которые дают нам положительное значение тангенса и два тупых — отрицательное значение тангенса.
Нам нужно найти наименьшее значение производной, поэтому мы ищем то значение, которое будет левее на числовой оси. Получается, что это будут отрицательные значения. Таким образом, рассмотрим только две точки — A и B и только тангенсы углов, которые дают нам касательные a и b. Для того, чтобы определить какой из этих углов даст нам больший тангенс, нарисуем вспомогательный тригонометрический круг, на котором отметим, примерно разумеется, значения углов и посмотрим на значения тангенсов. Просто перенесем эти две касательные на этот круг так, чтобы они проходили через его центр, но не изменяли наклона. Тангенс мы получаем равным длине отрезка на красной линии (ось тангенса) от оси абсцисс до точки пересечения с этой линией касательной. Мы видим, что наибольшее числовое значение тангенса будет у касательной b. Но так как у нас числа расположенные на числовой оси возрастают от наибольших отрицательных к наибольшим положительным, то наибольшее отрицательное число — будет как раз наименьшим значением производной.
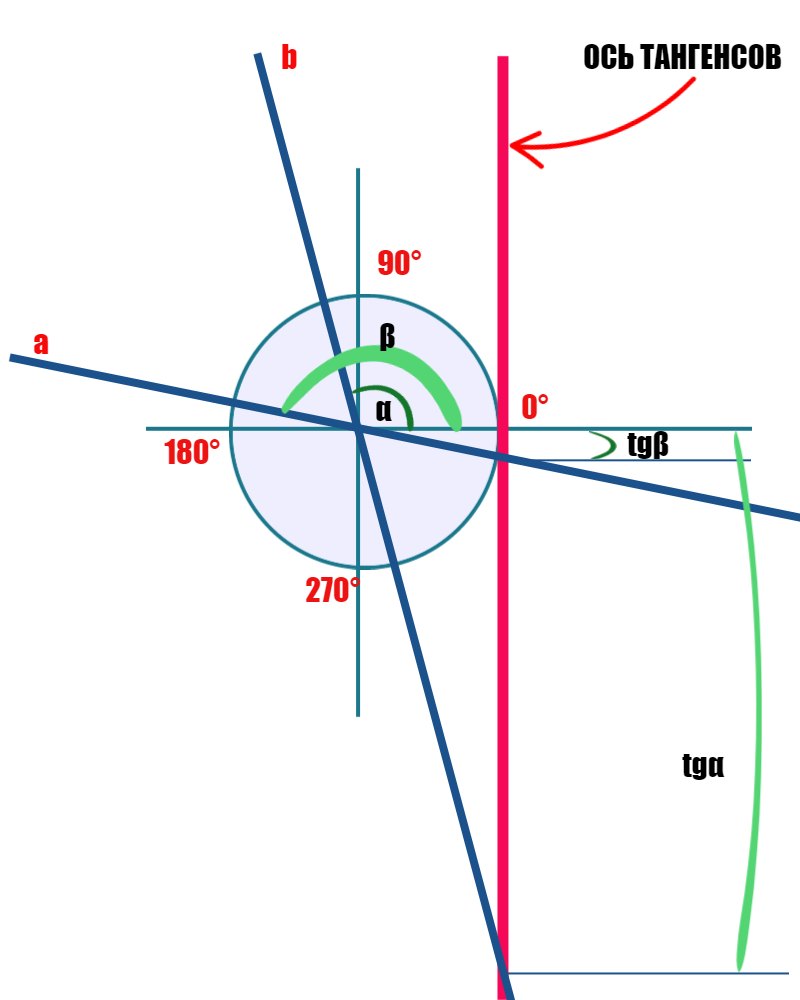
Таким образом, точка, при которой значение тангенса угла касательной к графику функции наименьшее, это точка с абсциссой -1.
Ответ: -1.
Рекомендуем для лучшего понимания изучить тему «Производная и ее геометрический смысл»









