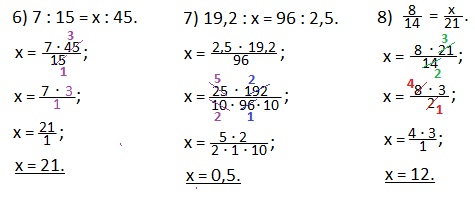Равенство двух отношений называют пропорцией.
Тема: «Отношение» рассмотрена на предыдущем занятии («6.1. Отношение»).
a:b=c:d. Это пропорция. Читают: а так относится к b, как c относится к d. Числа a и d называют крайними членами пропорции, а числа b и c – средними членами пропорции.
Пример пропорции: 12 : 3 = 16 : 4. Это равенство двух отношений: 12:3=4 и 16:4=4. Читают: двенадцать так относится к трем, как шестнадцать относится к четырем. Здесь 12 и 4 -крайние члены пропорции, а 3 и 16 - средние члены пропорции.
Основное свойство пропорции
Произведение крайних членов пропорции равно произведению ее средних членов.
Для пропорции a:b=c:d или a/b=c/d основное свойство записывается так: a·d=b·c.
Для нашей пропорции 12 : 3 = 16 : 4 основное свойство запишется так: 12·4=3·16. Получается верное равенство: 48=48.
Чтобы найти неизвестный крайний член пропорции, нужно произведение средних членов пропорции разделить на известный крайний член.
Примеры. Найти неизвестный крайний член пропорции.
1) х : 20 = 2 : 5. У нас х и 5 — крайние члены пропорции, а 20 и 2 — средние.
Решение.
х = (20·2):5 — нужно перемножить средние члены (20 и 2) и результат разделить на известный крайний член (число 5);
х = 40 : 5 — произведение средних членов (40) разделим на известный крайний член (5);
х = 8. Получили искомый крайний член пропорции.
Удобнее записывать нахождение неизвестного члена пропорции с помощью обыкновенной дроби. Вот как тогда запишется рассмотренный нами пример:
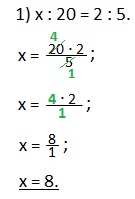Искомый крайний член пропорции (х) будет равен произведению средних членов (20 и 2), деленному на известный крайний член (5).
Сокращаем дробь на 5 (делим на 5 и числитель и знаменатель дроби). Находим значение х.
Если забыли, как сокращать обыкновенные дроби, то повторите тему: «5.4.2. Примеры сокращения обыкновенных дробей»
Еще такие примеры на нахождение неизвестного крайнего члена пропорции.
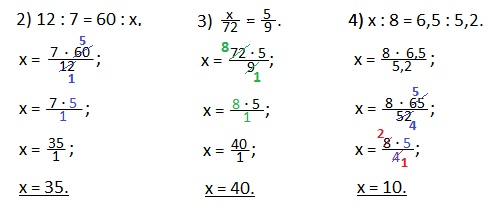
Чтобы найти неизвестный средний член пропорции, нужно произведение крайних членов пропорции разделить на известный средний член.
Примеры. Найти неизвестный средний член пропорции.
5) 9 : х = 3 : 14. Число 3 — известный средний член данной пропорции, числа 9 и 14 — крайние члены пропорции.
Решение.
х = (9·14):3 — перемножим крайние члены пропорции и результат разделим на известный средний член пропорции;
х= 136:3;
х=42.
Решение этого примера можно записать иначе:
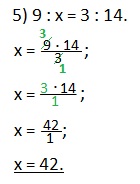Искомый средний член пропорции (х) будет равен произведению крайних членов (9 и 14), деленному на известный средний член (3).
Сокращаем дробь на 3 (делим на 3 и числитель и знаменатель дроби). Находим значение х.
Если забыли, как сокращать обыкновенные дроби, то повторите тему: «5.4.2. Примеры сокращения обыкновенных дробей»
Еще такие примеры на нахождение неизвестного среднего члена пропорции.
