Давайте рассмотрим варианты деления рациональных чисел.
Содержание
Деление отрицательных чисел
![]() Частное двух отрицательных чисел есть число положительное. Модуль частного равен частному модулей делимого и делителя.
Частное двух отрицательных чисел есть число положительное. Модуль частного равен частному модулей делимого и делителя.
Так как частное двух положительных чисел — это тоже число положительное, то делаем ВЫВОД:
Частное двух чисел с одинаковыми знаками есть число положительное. Модуль частного равен частному модулей делимого и делителя.
Пример 1
Выполнить деление (устно):
а) -24:(-10); б) -370: (-1000); в) -253: (-11); г) -18,72: (-6).
Решение. Знак результата «+» (по правилу деления отрицательных чисел). В примерах а) и б) используем правило деления числа на 10, 100, 1000 и т. д. Если забыли — смотрите здесь. В примере в) вспомните, как умножается двузначное число на 11 (цифры двузначного числа раздвигаются и между ними ставится число, равное сумме двух крайних цифр).
а) -24:(-10)=2,4; б) -370: (-1000)=0,37; в) -253: (-11)=23; г) -18,72: (-6)=3,12.
Пример 2
Вычислить:
Решение. По правилу деления отрицательных чисел результат будет положительным числом. Модуль частного в примерах а) и б) вычисляем по правилу деления на десятичную дробь. Повторить это можно здесь. В примерах в) и г) вначале обращаем смешанные числа в неправильные дроби, а затем используем правило деления обыкновенных дробей. Если забыли, как это делается — смотрите здесь!
Деление чисел с разными знаками
![]() Частное двух чисел с разными знаками есть число отрицательное. Модуль частного равен частному модулей делимого и делителя.
Частное двух чисел с разными знаками есть число отрицательное. Модуль частного равен частному модулей делимого и делителя.
ВЫВОД: и при умножении и при делении двух чисел с разными знаками — ответ будет со знаком «-».
Пример 3
Найти частное чисел:
Решение. Применяйте правила, решайте самостоятельно и только потом сверяйтесь с приведенным ниже решением.
Все получилось? Продолжим.
Пример 4
Вычислить:
Решайте и сверяйтесь!

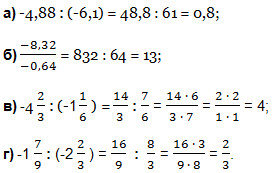
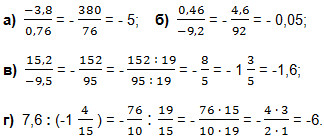
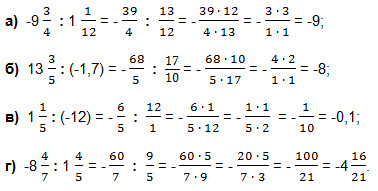






Отлично. Мне очень помогло в учебе.