I. ax2+bx+c=0 – квадратное уравнение общего вида
Дискриминант D=b2— 4ac.
Если D>0, то имеем два действительных корня:
Если D=0, то имеем единственный корень (или два равных корня) х=-b/(2a).
Если D<0, то действительных корней нет.
Пример 1) 2x2+5x-3=0.
Решение. a=2; b=5; c=-3.
D=b2— 4ac=52-4∙2∙(-3)=25+24=49=72>0; 2 действительных корня.
Пример 2) 4x2+21x+5=0.
Решение. a=4; b=21; c=5.
D=b2— 4ac=212— 4∙4∙5=441-80=361=192>0; 2 действительных корня.
II. ax2+bx+c=0 – квадратное уравнение частного вида при четном втором
коэффициенте b
Пример 3) 3x2-10x+3=0.
Решение. a=3; b=-10 (четное число); c=3.
Пример 4) 5x2-14x-3=0.
Решение. a=5; b= -14 (четное число); c=-3.
Пример 5) 71x2+144x+4=0.
Решение. a=71; b=144 (четное число); c=4.
Пример 6) 9x2-30x+25=0.
Решение. a=9; b=-30 (четное число); c=25.
III. ax2+bx+c=0 – квадратное уравнение частного вида при условии: a-b+c=0.
Первый корень всегда равен минус единице, а второй корень равен минус с, деленному на а:
x1=-1, x2=-c/a.
Пример 7) 2x2+9x+7=0.
Решение. a=2; b=9; c=7. Проверим равенство: a-b+c=0. Получаем: 2-9+7=0.
Тогда x1=-1, x2=-c/a=-7/2=-3,5. Ответ: -1; -3,5.
IV. ax2+bx+c=0 – квадратное уравнение частного вида при условии: a+b+c=0.
Первый корень всегда равен единице, а второй корень равен с, деленному на а:
x1=1, x2=c/a.
Пример 8 ) 2x2-9x+7=0.
Решение. a=2; b=-9; c=7. Проверим равенство: a+b+c=0. Получаем: 2-9+7=0.
Тогда x1=1, x2=c/a=7/2=3,5. Ответ: 1; 3,5.

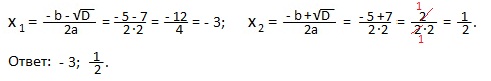
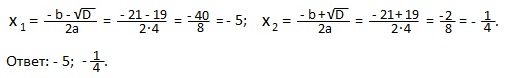

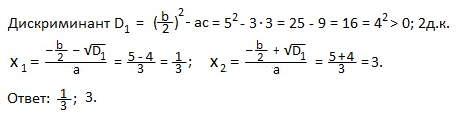
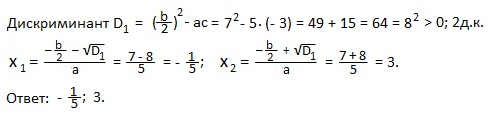
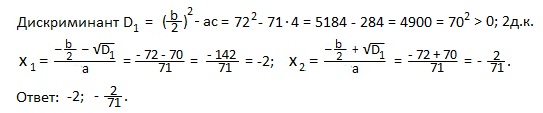
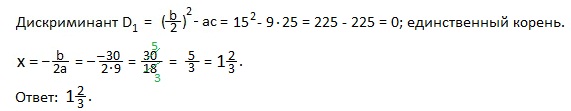




В первом будет -3, 2/4.
2/4 можно сократить на 2, получится ½.