Квадратный трехчлен ax2+bx+c можно разложить на линейные множители по формуле:
ax2+bx+c=a (x-x1)(x-x2), где x1, x2 — корни квадратного уравнения ax2+bx+c=0.
Разложить квадратный трехчлен на линейные множители:
Пример 1). 2x2-7x-15.
Решение. Найдем корни квадратного уравнения: 2x2-7x-15=0.
a=2; b=-7; c=-15. Это общий случай для полного квадратного уравнения. Находим дискриминант D.
D=b2-4ac=(-7)2-4∙2∙(-15)=49+120=169=132>0; 2 действительных корня.
Применим формулу: ax2+bx+c=a (x-x1)(x-x2).
2x2-7x-15=2 (х+1,5)(х-5)=(2х+3)(х-5). Мы представили данный трехчлен 2x2-7x-15 в виде произведения двучленов 2х+3 и х-5.
Ответ: 2x2-7x-15=(2х+3)(х-5).
Пример 2). 3x2+2x-8.
Решение. Найдем корни квадратного уравнения:
3x2+2x-8=0.
a=3; b=2; c=-8. Это частный случай для полного квадратного уравнения с четным вторым коэффициентом (b=2). Находим дискриминант D1.
Применим формулу: ax2+bx+c=a (x-x1)(x-x2).
Мы представили трехчлен 3x2+2x-8 в виде произведения двучленов х+2 и 3х-4.
Ответ: 3x2+2x-8=(х+2)(3х-4).
Пример 3). 5x2-3x-2.
Решение. Найдем корни квадратного уравнения:
5x2-3x-2=0.
a=5; b=-3; c=-2. Это частный случай для полного квадратного уравнения с выполненным условием: a+b+c=0 (5-3-2=0). В таких случаях первый корень всегда равен единице, а второй корень равен частному от деления свободного члена на первый коэффициент:
Применим формулу: ax2+bx+c=a (x-x1)(x-x2).
5x2-3x-2=5 (х-1)(х+0,4)=(х-1)(5х+2). Мы представили трехчлен 5x2-3x-2 в виде произведения двучленов х-1 и 5х+2.
Ответ: 5x2-3x-2=(х-1)(5х+2).
Пример 4). 6x2+x-5.
Решение. Найдем корни квадратного уравнения:
6x2+x-5=0.
a=6; b=1; c=-5. Это частный случай для полного квадратного уравнения с выполненным условием: a-b+c=0 (6-1-5=0). В таких случаях первый корень всегда равен минус единице, а второй корень равен минус частному от деления свободного члена на первый коэффициент:
Применим формулу: ax2+bx+c=a (x-x1)(x-x2).
Мы представили трехчлен 6x2+x-5 в виде произведения двучленов х+1 и 6х-5.
Ответ: 6x2+x-5=(х+1)(6х-5).
Пример 5). x2-13x+12.
Решение. Найдем корни приведенного квадратного уравнения:
x2-13x+12=0. Проверим, можно ли применить теорему Виета. Для этого найдем дискриминант и убедимся, что он является полным квадратом целого числа.
a=1; b=-13; c=12. Находим дискриминант D.
D=b2-4ac=132-4∙1∙12=169-48=121=112.
Применим теорему Виета: сумма корней должна быть равна второму коэффициенту, взятому с противоположным знаком, а произведение корней должно быть равно свободному члену:
x1+x2=13; x1∙x2=12. Очевидно, что x1=1; x2=12.
Применим формулу: ax2+bx+c=a (x-x1)(x-x2).
x2-13x+12=(х-1)(х-12).
Ответ: x2-13x+12=(х-1)(х-12).
Пример 6). x2-4x-6.
Решение. Найдем корни приведенного квадратного уравнения:
x2-4x-6=0.
a=1; b=-4; c=-6. Второй коэффициент — четное число. Находим дискриминант D1.
Дискриминант не является полным квадратом целого числа, поэтому, теорема Виета нам не поможет, и мы найдем корни по формулам для четного второго коэффициента:
Применим формулу: ax2+bx+c=a (x-x1)(x-x2) и запишем ответ:
Друзья, для того, чтобы разложить квадратные трехчлены на множители, мы решали каждое квадратное уравнение рациональным способом. Все эти способы мы рассмотрели ранее в теме: «Решение полных квадратных уравнений».

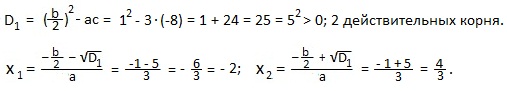




Вы супер объясняете. Мой бы учитель нормально обяснял было бы лучше.