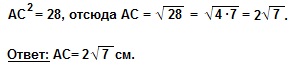Теорема Пифагора.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
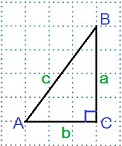
Катеты АС и ВС, гипотенуза АВ.
АВ²=АС²+ВС² или АС²+ВС²=АВ².
Если АС=b, BC=a, AB=c, то c²=a²+b² или a²+b²=c².
Египетский треугольник — это прямоугольный треугольник со сторонами 3, 4 и 5.
3²+4²=5². На рисунке (выше) показан египетский треугольник.
Задача. Две стороны прямоугольного треугольника равны 6 см и 8 см. Найти третью сторону. (Рассмотреть два случая).
1 случай. Пусть две данные стороны — катеты прямоугольного треугольника.
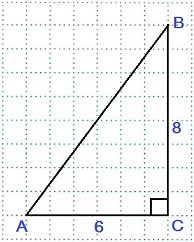Дано: в Δ АВС / C=90º, АС=6 см, ВС=8 см.
Найти АВ.
Решение. По теореме Пифагора:
АВ²=АС²+ВС²;
АВ²=6²+8²;
АВ²=36+64;
Ответ: АВ=10 см.
2 случай. Пусть две данные стороны — катет и гипотенуза прямоугольного треугольника.
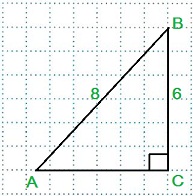Дано: в Δ АВС / C=90º, ВС=6 см, АВ=8 см.
Найти АС.
Решение. По теореме Пифагора:
АВ²=АС²+ВС²;
8²=АС²+6²;
64=АС²+36; АС²=64-36;
