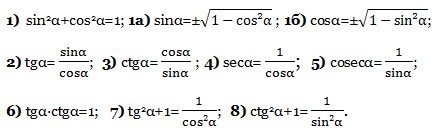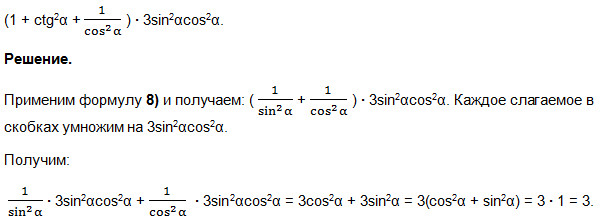8.2.4. Основные тригонометрические тождества. Часть 1

Основные тригонометрические тождества.

secα читают: «секанс альфа». Это число, обратное косинусу альфа.

соsecα читают: «косеканс альфа». Это число, обратное синусу альфа.

Примеры. Упростить выражение:

а) 1 – sin²α; б) cos²α – 1; в) (1 – cosα)(1+cosα); г) sin²αcosα – cosα; д) sin²α+1+cos²α;

е) sin⁴α+2sin²αcos²α+cos⁴α; ж) tg²α – sin²αtg²α; з) ctg²αcos²α – ctg²α; и) cos²α+tg²αcos²α.

Решение.

а) 1 – sin²α = cos²α по формуле 1);

б) cos²α – 1 =- (1 – cos²α) = -sin²α также применили формулу 1);

в) (1 – cosα)(1+cosα) = 1 – cos²α = sin²α. Вначале мы применили формулу разности квадратов двух выражений: (a – b)(a+b) = a² – b², а затем формулу 1);

г) sin²αcosα – cosα. Вынесем общий множитель за скобки.

sin²αcosα – cosα = cosα(sin²α – 1) = -cosα(1 – sin²α) = -cosα ∙ cos²α = -cos³α. Вы, конечно, уже заметили, что так как 1 – sin²α = cos²α, то sin²α – 1 = -cos²α. Точно так же, если 1 – cos²α = sin²α, то cos²α – 1 = -sin²α.

д) sin²α+1+cos²α = (sin²α+cos²α)+1 = 1+1 = 2;

е) sin⁴α+2sin²αcos²α+cos⁴α. Имеем: квадрат выражения sin²α плюс удвоенное произведение sin²α на cos²α и плюс квадрат второго выражения cos²α. Применим формулу квадрата суммы двух выражений: a²+2ab+b²=(a+b)². Далее применим формулу 1). Получим:  sin⁴α+2sin²αcos²α+cos⁴α = (sin²α+cos²α)² = 1² = 1;

ж) tg²α – sin²αtg²α = tg²α(1 – sin²α) = tg²α ∙ cos²α = sin²α. Применили формулу 1), а затем формулу 2).

Запомните: tgα ∙ cosα = sinα.

Аналогично, используя формулу  3) можно получить: ctgα ∙ sinα = cosα. Запомнить!

з) ctg²αcos²α – ctg²α = ctg²α(cos²α – 1) = ctg²α ∙ (-sin²α) = -cos²α.

и) cos²α+tg²αcos²α = cos²α(1+tg²α) = 1. Мы вначале вынесли общий множитель за скобки, а содержимое скобок упростили по формуле 7).

Преобразовать выражение:

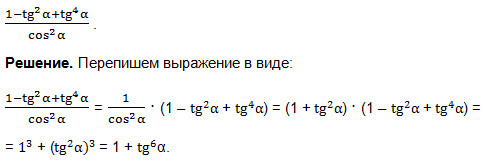
Мы применили формулу 7) и получили произведение суммы двух выражений на неполный квадрат разности этих выражений – формулу суммы кубов двух выражений:

a³ + b³ = (a + b)(a² – ab + b²). У нас а = 1, b = tg²α.

Упростить: