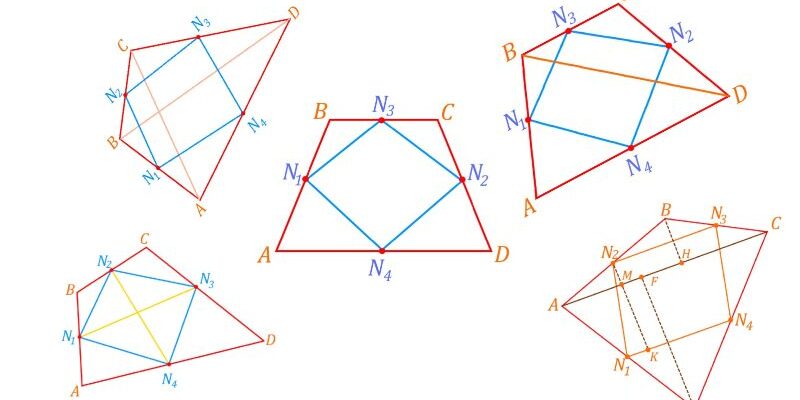
Эта фигура не самостоятельна, она образуется из выпуклого четырехугольника, если соединить в нем точки — середины сторон. На рисунке ![]() — параллелограмм Вариньона. Эту геометрическую фигуру изучают по геометрии в 8 классе.
— параллелограмм Вариньона. Эту геометрическую фигуру изучают по геометрии в 8 классе.
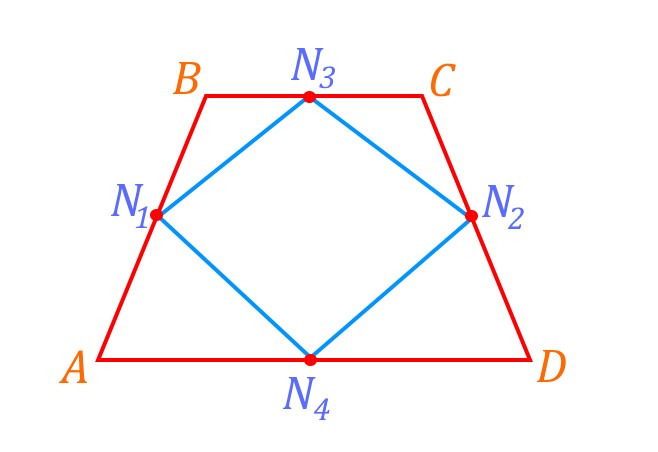
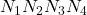 параллелограмм Вариньона
параллелограмм Вариньона
Параллелограмм открыл французский математик Пьер Вариньон (1654 — 1722). Соединив середины сторон выпуклого четырехугольника, математик получил еще один четырехугольник. Вариньон доказал, что полученный четырехугольник является параллелограммом и описал его свойства. Это удивительное свойство любого четырехугольника — середины его сторон образуют всегда параллелограмм. Открытие Вариньона было опубликовано посмертно в 1731 году. Оно такое простое, что кажется странным — почему оно не было открыто гораздо раньше. Как мы знаем — все гениальное — просто.
Диагонали параллелограмма Вариньона соединяют середины противоположных сторон исходного четырехугольника и называются бимедианами.
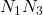 и
и 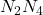 )
)Содержание
Теорема Вариньона
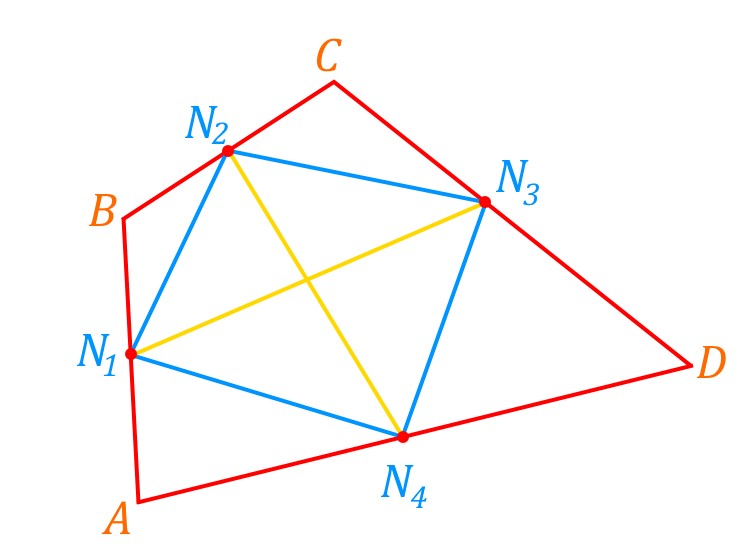
Доказать, что ![]() , вершинами которого являются точки — середины сторон выпуклого четырехугольника
, вершинами которого являются точки — середины сторон выпуклого четырехугольника ![]() , параллелограмм.
, параллелограмм.
Доказательство
Соединим точки ![]() и
и ![]() и рассмотрим треугольники
и рассмотрим треугольники ![]() и
и ![]() . Они имеют общее основание
. Они имеют общее основание ![]() .
.
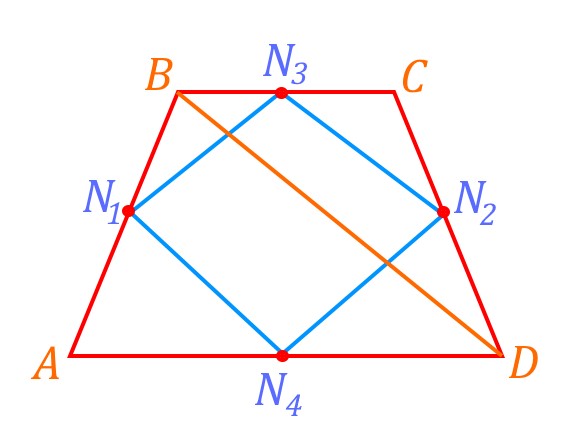
![]() — средняя линия треугольника
— средняя линия треугольника ![]() ,
, ![]() — средняя линия треугольника
— средняя линия треугольника ![]() Так как в треугольника средняя линия параллельна основанию и равна его половине, то
Так как в треугольника средняя линия параллельна основанию и равна его половине, то ![]() и
и ![]() параллельны основанию
параллельны основанию ![]() и равны его половине, а, значит, они параллельны между собой и равны.
и равны его половине, а, значит, они параллельны между собой и равны.
Аналогично доказывается параллельность и равенство ![]() и
и ![]() .
.
Получается в четырехугольнике ![]() противоположные стороны равны и параллельны. Это параллелограмм.
противоположные стороны равны и параллельны. Это параллелограмм.
Теорема доказана.
Свойства параллелограмма Вариньона
Свойство 1
Стороны параллелограмма Вариньона параллельны диагоналям любого выпуклого четырехугольника и равны их половинам.
Доказательство:
Нарисуем произвольный выпуклый четырехугольник ![]() , проведем в нем диагонали и отметим точки — середины сторон. Соединим эти точки, получим параллелограмм Вариньона
, проведем в нем диагонали и отметим точки — середины сторон. Соединим эти точки, получим параллелограмм Вариньона ![]() .
.
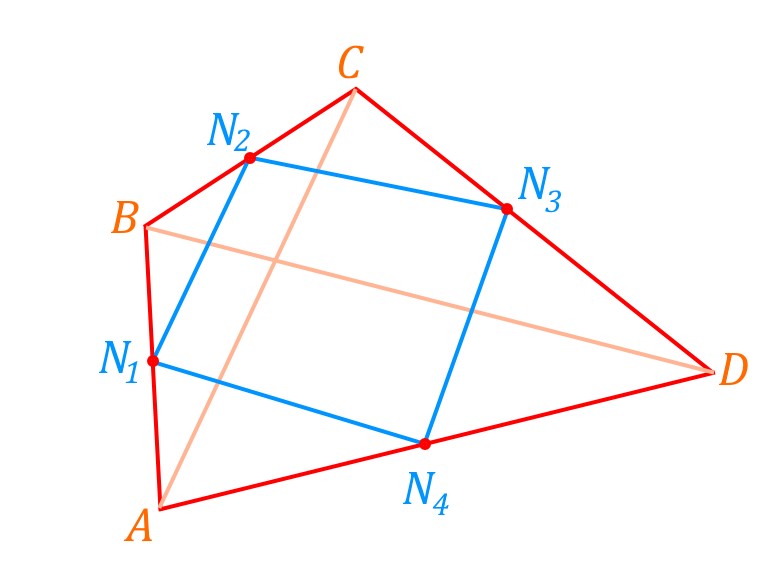
Докажем, что ![]() и
и ![]() и что
и что ![]() и
и ![]() .
.
Из доказательства данных утверждений будут следовать доказательства следующих утверждений, так как ![]() параллелограмм:
параллелограмм:
![]() и
и ![]() и что
и что ![]() и
и ![]() .
.
Действительно, рассмотрим треугольник ![]() — в нем
— в нем ![]() является средней линией (по построению), тогда
является средней линией (по построению), тогда ![]() и
и ![]() (по свойству средней линии треугольника).
(по свойству средней линии треугольника).
Рассмотрим теперь треугольник ![]() — в нем
— в нем ![]() — средняя линия. И по свойству средней линии треугольника следует, что
— средняя линия. И по свойству средней линии треугольника следует, что ![]() и
и ![]() .
.
Таким образом, данное свойство доказано.
Следующие свойства вы сможете доказать самостоятельно.
Свойство 2
Если диагонали исходного четырехугольника пересекаются под прямым углом, то параллелограмм Вариньона является прямоугольником.
Свойство 3
Площадь параллелограмма Вариньона в два раза меньше площади исходного четырехугольника.
Докажем это утверждение.
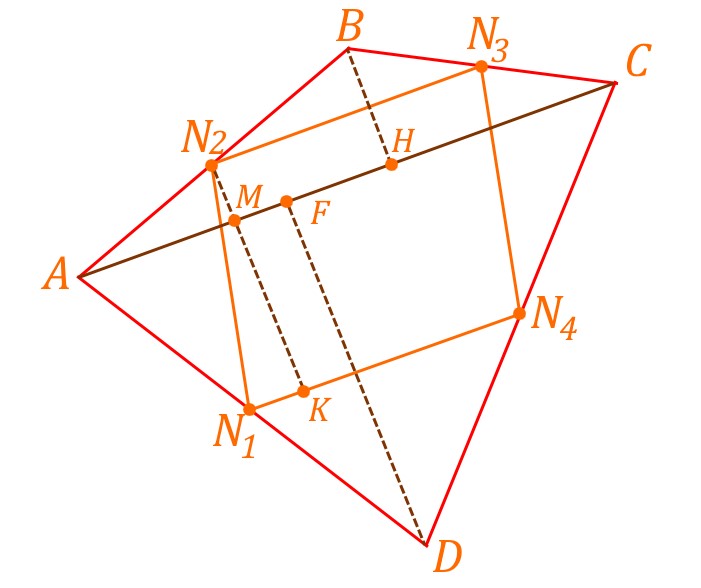
Нарисуем четырехугольник ![]() и в нем наш параллелограмм
и в нем наш параллелограмм ![]() . Соединим точки
. Соединим точки ![]() и
и ![]() . Проведем высоту
. Проведем высоту ![]() и высоты треугольников
и высоты треугольников ![]() и
и ![]() —
— ![]() и
и ![]() . Точка
. Точка ![]() — точка пересечения высоты
— точка пересечения высоты ![]() и диагонали
и диагонали ![]() .
.
![]() .
.
Так как ![]() , а также
, а также ![]() , то получим:
, то получим:
![]()
Раскроем скобки:
![]()
Так как ![]() и
и ![]() , получаем:
, получаем:
![]()
![]()
![]() .
.
Свойство 4
Периметр параллелограмма Вариньона, равен сумме диагоналей исходного четырехугольника.
Действительно — каждая из сторон параллелограмма равна половине диагонали четырехугольника, которой она параллельна. Так как является средней линией треугольника с основанием совпадающем с диагональю.
Знание о существовании такого замечательного параллелограмма внутри каждого выпуклого четырехугольника помогает быстро решать множество геометрических задач. И нет необходимости сначала доказывать, что такая фигура является параллелограммом и что ее площадь равно половине площади исходного четырехугольника.

Благодарю за ценную информацию