В 8 классе по алгебре начинают изучать квадратные уравнения и самый популярный способ их решения - через дискриминант. Формула вычисления дискриминанта известна
![]()
Дискриминант в математике используется чтобы определить сколько корней в уравнении — 1 корень, 2 корня или действительных корней нет. В этой статье определим, что такое дискриминант и выведем формулу дискриминанта.
Содержание
Определение
Определим что такое дискриминант и зачем он нужен в математике, а также как его рассчитать.
Дискриминантом называют число, описывающее свойство коэффициентов квадратного многочлена. Хотя есть дискриминанты и кубических многочленов.
По этому числу определяют характер корней уравнения, полученному если многочлен приравнять к нулю. Так, если дискриминант больше нуля, то уравнение будет иметь два корня, равен нулю, то 1 корень, а если будет меньше нуля, то корней не будет.
Дискриминант (определение) помогает определить наличие или отсутствие корней квадратного уравнения, не решая его.
Обозначается дискриминант квадратного уравнения буквой
или знаком Δ. И находится по формуле:
D=b^2-4ac , где
,
и
— коэффициенты уравнения:
ax^2+bx+c=0
Корни через дискриминант определяются по формулам:
\displaystyle x_1=\frac{-b-\sqrt{D}}{2a} и \displaystyle x_2=\frac{-b+\sqrt{D}}{2a}
Пример вычисления дискриминанта:
Вычислим дискриминант в уравнении 6x^2+4x+2=0 .
По формуле находим:
D=b^2-4ac=4^2-4\cdot 6 \cdot 2=16-48=-32
Мы получили отрицательный дискриминант, значит, данное уравнение не имеет действительных корней. Действительно, так как корни квадратного уравнения находят по формулам:
\displaystyle x_1=\frac{-b-\sqrt{D}}{2a} и \displaystyle x_2=\frac{-b+\sqrt{D}}{2a}
Подставим значения для исходного уравнения:
\displaystyle x_1=\frac{-4-\sqrt{-32}}{12} и \displaystyle x_2=\frac{-4+\sqrt{-32}}{12}
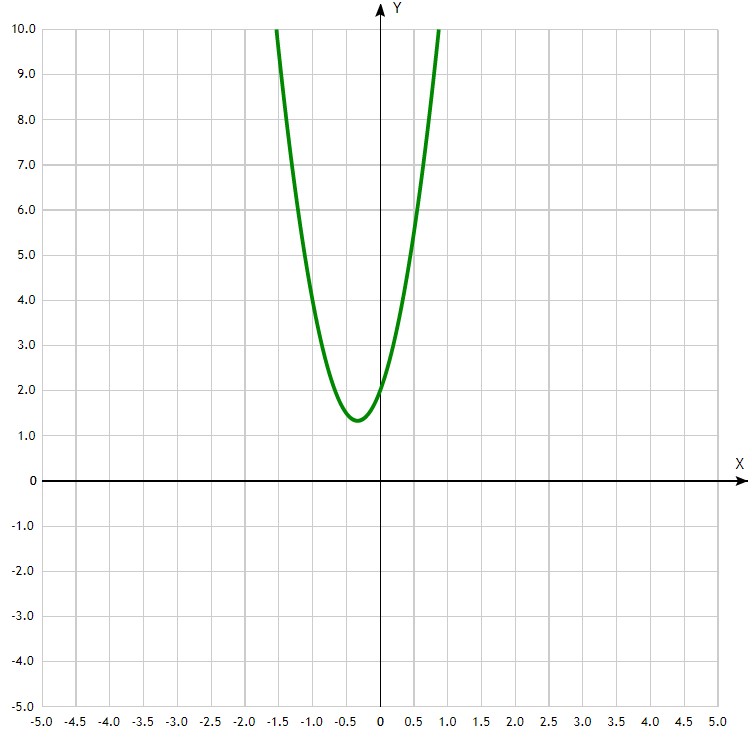
Как видим, мы никак не сможем посчитать корни — у нас отрицательное число под знаком радикала. И, действительно, если вы построите график функции f (x)=6x^2+4x+2 — он нигде не пересечет ось ![]() , то есть ни при каком
, то есть ни при каком ![]() мы не получим ноль.
мы не получим ноль.
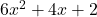
Геометрический смысл дискриминанта
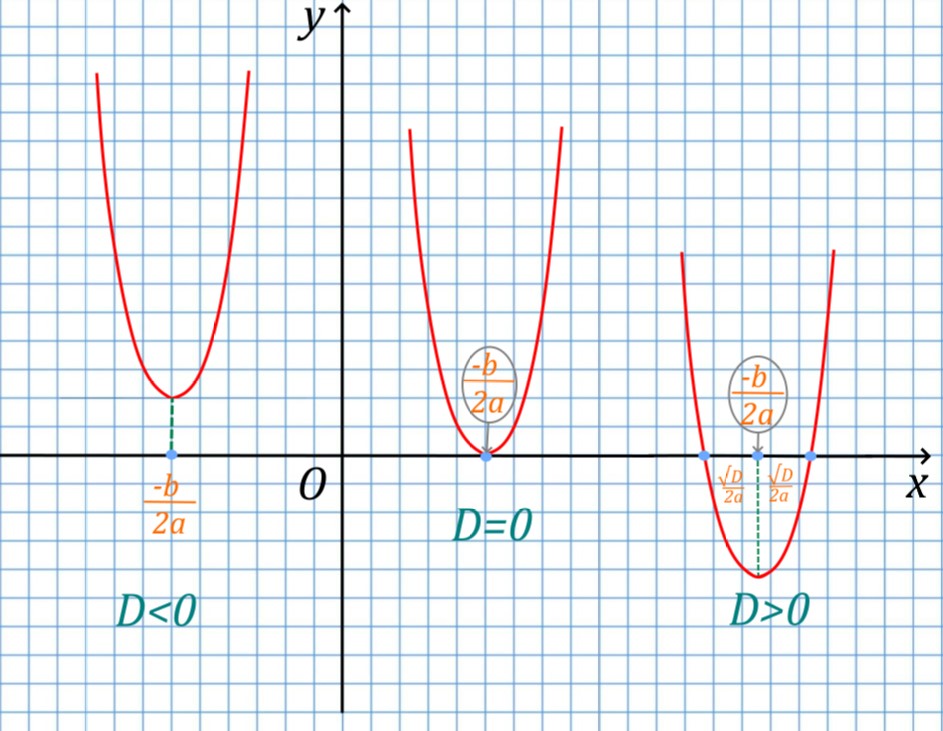
Что означает дискриминант на графике, каков его геометрический смысл? Графически дискриминант квадратного уравнения характеризует расстояние по оси абсцисс между точкой — вершиной параболы (парабола — график квадратичной функции) и точкой пересечения графика с осью абсцисс. Посмотрите на рисунок. На нем видно:
- Если дискриминант равен нулю (D=0), это значит, что вершина параболы и является точкой пересечения с осью абсцисс — расстояние между точкой пересечения и вершиной параболы равно нулю.
- Когда D>0, то справа и слева от точки абсцисс вершины параболы на одинаковом расстоянии \displaystyle \frac{\sqrt{D}}{2a} будут находиться точки пересечения параболы ax^2+bx+c=y, которые являются корнями уравнения ax^2+bx+c=0.
- Когда D<0 — это означает, что точек действительных отметить на оси абсцисс нельзя, то есть от вершины отложить расстояние до точек пересечения графика с осью абсцисс невозможно, то есть этих точек пересечения нет. График не пересекает ось абсцисс и корней уравнения [katex]ax^2+bx+c=0[/katex] нет.
Корни квадратного уравнения через дискриминант.
Полное квадратное уравнение
Пусть нам дано уравнение вида ax^2+bx+c=0. Вычисляем дискриминант по известной формуле. Затем определяем корни уравнения.
- Если D>0 получаем два вещественных корня \displaystyle x_1=\frac{-b-\sqrt{D}}{2a} и \displaystyle x_2=\frac{-b+\sqrt{D}}{2a}.
- Если D=0 корни будут совпадать: \displaystyle x_1=x_2=\frac{-b}{2a}
- Если D<0, вещественных корней нет, но есть мнимые корни или так называемые комплексные корни (обычно изучаются в курсе математического анализа в ВУЗах, хотя иногда и встречаются в алгебре 9-11 классов).
Неполное квадратное уравнение
Неполным называется такое квадратное уравнение, когда один из коэффициентов такого уравнения равен нулю.
- Пусть коэффициент a=0, тогда уравнение сводится к линейному уравнению вида kx+b=0 и уже не будет считаться неполным.
- Если равны нулю два коэффициента:
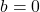 и
и 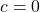 , тогда
, тогда 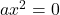 . Решением такого уравнения будет:
. Решением такого уравнения будет: 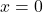 .
. - Если равен нулю коэффициент b, то имеем D=-4ac и \displaystyle x_1= \frac{\sqrt{D}}{2a} и \displaystyle x_2= -\frac{\sqrt{D}}{2a}.
- При равенстве нулю свободного члена c=0 имеем D=b^2 и \displaystyle x_1=\frac{-b-\sqrt{D}}{2a} и \displaystyle x_2=\frac{-b+\sqrt{D}}{2a}.
Приведенное квадратное уравнение
Приведенным квадратным уравнением называется такое уравнение вида ![]() , в котором старший коэффициент равен a=1. Оно решается обычно по теореме Виета.
, в котором старший коэффициент равен a=1. Оно решается обычно по теореме Виета.
Дискриминант находится по формуле: ![]() .
.
Если второй коэффициент кратен 2
Если коэффициент b можно разделить на 2 (с четным вторым коэффициентом), то тогда вычисляется не полный дискриминант, а \displaystyle \frac{D}{4} по формуле:
\displaystyle \frac{D}{4}=\left ( \frac{b}{2} \right)^2-ac,
а корни: \displaystyle x_1=\frac{-\frac{b}{2}-\sqrt{\frac{D}{4}}}{a} и второй корень \displaystyle x_2=\frac{-\frac{b}{2}+\sqrt{\frac{D}{4}}}{a}.
Примеры нахождения корней уравнения с помощью дискриминанта
Пример 1
Решим уравнение: 4x^2+5x-5=0
Находим дискриминант: D=25-4 \cdot 4 \cdot (-5)=25+80=105
Корни: \displaystyle x_1=\frac{-5-\sqrt{105}}{2\cdot 4}, \displaystyle x_2=\frac{-5+\sqrt{105}}{2\cdot 4}
или
\displaystyle x_1=\frac{-5-\sqrt{105}}{8}, \displaystyle x_2=\frac{-5+\sqrt{105}}{8}
Пример 2
Сколько корней в данном уравнении 2x^2-3x+6=0?
Для ответа на этот вопрос необходимо найти дискриминант:
D=3^2-4 \cdot 2 \cdot 6=9-48=-39
D<0[/katex] — действительных корней нет.</p> <h3>Пример 3</h3> <p>[katex]x^2-6x-72=0 — найти корень.
D=b^2-4ac=(-6)^2-4 \cdot (-72)=36+288=324
Так как ![]() , имеем два корня:
, имеем два корня:
\displaystyle x_1=\frac{6-\sqrt{324}}{2}, x_2=\frac{6+\sqrt{324}}{2}
\displaystyle x_1=\frac{6-18}{2}=-6, x_2=\frac{6+18}{2}=12
Пример 4
Решить неполное уравнение
x^2-4=0
Способ 1
Разложим левую часть по формуле разность квадратов:
(x-2)(x+2)=0
Тогда корни:
x_1=-2, x_2=2
Способ 2
Решим задачу с помощью дискриминанта: ![]() , тогда \displaystyle x_1=\sqrt{D}/2=\sqrt{16}/2=4/2=2,
, тогда \displaystyle x_1=\sqrt{D}/2=\sqrt{16}/2=4/2=2,
\displaystyle x_2=-\sqrt{D}/2=-\sqrt{16}/2=-4/2=-2
Пример 5
Придумайте такое квадратное уравнение, в котором будет нулевой дискриминант.
Решение:
Так как формула дискриминанта: D=b^2-4ac, то выберем любые коэффициенты ![]() и
и ![]() , а
, а ![]() найдем, если приравняем D=b^2-4ac к нулю.
найдем, если приравняем D=b^2-4ac к нулю.
Пусть ![]() , a
, a ![]() , тогда \displaystyle D=4^2-4\cdot 7\cdot c=0
, тогда \displaystyle D=4^2-4\cdot 7\cdot c=0
4^2-4\cdot 7\cdot c=0
16-28c=0
-28c=-16 Разделим левую и правую части на -4.
7c=4
\displaystyle c=\frac{4}{7}
И, получаем: \displaystyle 7x^2+4x+\frac{4}{7}=0
Ответ: \displaystyle 7x^2+4x+\frac{4}{7}=0
Выводы
Самое важное, что надо запомнить, это формулу:
D=b^2-4ac
и как определяются корни квадратного уравнения:
\displaystyle x_1=\frac{-b-\sqrt{D}}{2a} и \displaystyle x_2=\frac{-b+\sqrt{D}}{2a}
Можно забыть, как определяются корни в разных видах квадратных уравнений, неполных, приведенных, но если вы знаете главное — как определяется дискриминант и корни в полном квадратном уравнении, то вы сможете решить любое уравнение второй степени.




Слово обозначает «отличие», отличительные признаки многочлена от любого другого.
Скажите, пожалуйста, как именно дискриминант определяет, есть корни у уравнения или нет?
Если D>0, то 2 различных корня, если D=0, то корни совпадают (одно значение), если D<0, то действительных корней нет. В тексте смотрите раздел «Полное квадратное уравнение».
Это да, это я понимаю, но почему если D>0 , то число корней 2? Почему если D= 0, то корень 1 и если D<0, то нет корней? Как люди поняли, что это так?
В тексте есть графики — на них видно, что означает дискриминант. Поняли, как я думаю, на постоянных тренировках в решении уравнений и рисовании их графиков.
Есть еще дискриминант гамильтониана.
Дискриминант гамильтониана физической системы зависит от конкретной рассматриваемой системы. В общем, гамильтониан представляет собой математическое представление энергии системы и обычно является функцией координат и импульсов системы.
Например, в случае атома водорода гамильтониан дается выражением:
H = — (1/2m)(d^2/dx^2) — (Ze^2/r)
Где m — масса электрона, e — заряд электрона, Z — атомный номер, r — расстояние между электроном и ядром.
Дискриминант этого гамильтониана можно вычислить, взяв определитель матрицы, образованной частными производными второго порядка от H по координатам и импульсам. Так что в этом случае дискриминант гамильтониана атома водорода равен нулю.
Стоит отметить, что формулы для гамильтониана и дискриминанта могут быть разными для разных систем и в разных областях физики. Гамильтониан часто определяется для конкретных систем, и дискриминант рассчитывается соответствующим образом.
Дополню тему, не смог пройти мимо этой прекрасной темы — посвятил изучению дискриминанта в разных областях знаний всю свою жизнь. Напишу про дискриминант кубического уравнения.
Кубическое уравнение — это уравнение вида ax^3 + bx^2 + cx + d = 0, где a, b, c и d — коэффициенты.
Дискриминант кубического уравнения — это величина, которая может быть вычислена из коэффициентов уравнения и дает информацию о характере решений уравнения.
Дискриминант кубического уравнения определяется выражением:
D = b ^ 2c ^ 2 — 4ac ^ 3 — 4b ^ 3d — 27a ^ 2d ^ 2 + 18abcd
Это выражение представляет собой полином от коэффициентов a, b, c и d. Его можно использовать для определения количества и характера решений кубического уравнения.
Многочлен четвертой степени — это уравнение вида ax^4 + bx^3 + cx^2 + dx + e = 0, где a, b, c, d и e — коэффициенты. Дискриминант полинома четвертой степени – это величина, которая вычисляется из коэффициентов уравнения и дает информацию о характере решений уравнения.
Дискриминант полинома четвертой степени определяется выражением:
D = 256a^3e^3 + 192a^2bde^2 — 128a^2c^2e^2 — 144a^2cd^2e + 27a^2d^4 + 144ab^2ce^2 — 6ab^2d^3 — 80abc^2de + 18abcd^3 + 16ac^4e — 4ac^3d^2 — 27b^4e^2 + 18b^3cde — 4b^3d^3 — 4b^2c^3e + b^2c^2d^2
Это выражение представляет собой полином от коэффициентов a, b, c, d и e. С его помощью можно определить количество и характер решений многочлена четвертой степени.
Если дискриминант положителен, уравнение имеет четыре различных действительных решения; если дискриминант равен нулю, уравнение имеет два повторяющихся действительных решения или одно повторяющееся действительное решение и одно другое действительное решение; если дискриминант отрицателен, уравнение имеет либо четыре комплексных решения, либо два действительных и два комплексно-сопряженных решения.