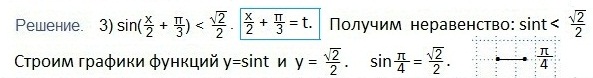На этом и последующих занятиях мы будем решать графическим способом тригонометрические неравенства одного какого-то вида. Сегодня мы решим три тригонометрических неравенства вида sint < a. Вот они:
Составим алгоритм решения.
1. Если аргумент — сложный (отличен от х), то заменяем его на t.
2. Строим в одной координатной плоскости tOy графики функций y=sint и y=a.
3. Находим такие две соседние точки пересечения графиков (поближе к оси Оу), между которыми синусоида располагается ниже прямой у=а. Находим абсциссы этих точек.
4. Записываем двойное неравенство для аргумента t, учитывая период синуса (t будет между найденными абсциссами).
5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.
Решение тригонометрических неравенств с помощью графиков надежно страхует нас от ошибок только в том случае, если мы грамотно построим синусоиду.
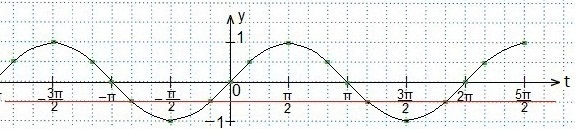
Решим первое неравенство
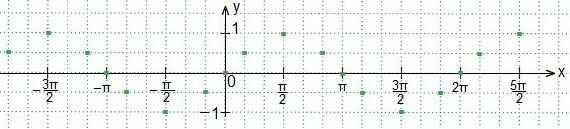
Для построения графика функции y=sinx выберем единичный отрезок, равный двум клеткам. Тогда по горизонтальной оси Ох значение π (≈3,14) составит шесть клеток. Рассчитываем остальные значения аргументов (в клетках).
Вот как будет выглядеть координатная плоскость.
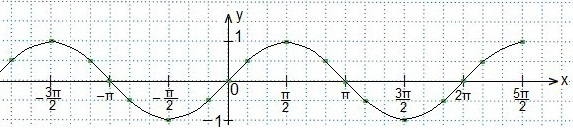
Эти точки мы взяли из таблицы значений синуса. 
Также используем свойство нечетности функции y=sinx (sin (-x)=-sinx), периодичность синуса (наименьший период Т=2π) и известное равенство: sin (π-x)=sinx. Проводим синусоиду
.
Проводим прямую.
Теперь нам предстоит определить такие две точки пересечения синусоиды и прямой, между которыми синусоида располагается ниже, чем прямая. Крайняя точка справа определена, абсцисса ближайшей искомой отстоит от начала отсчета влево на 8 клеток. Построим ее и определим.
Между этими (выделенными) значениями аргумента и находится та часть синусоиды, которая лежит ниже данной прямой, а значит, промежуток между этими выделенными точками удовлетворяет данному неравенству. Учтем период синуса, запишем результат в виде двойного неравенства, а ответ в виде числового промежутка.
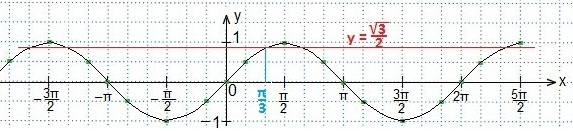
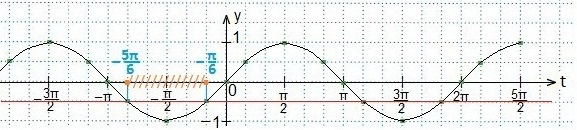
Решим второе неравенство
Синусоиду строим так же, а прямая будет параллельна оси Оt и отстоять от нее на 1 клетку вниз.
Определяем промежуток, внутри которого точки синусоиды лежат ниже прямой.
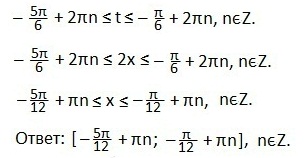Записываем промежуток значений введенной переменной t. Возвращаемся к первоначальному значению аргумента (2х). Все части двойного неравенства делим на 2 и определяем промежуток значений х. Записываем ответ в виде числового промежутка.
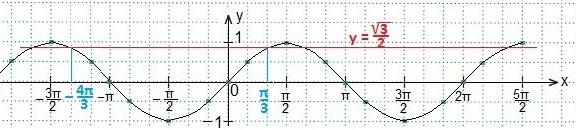
Аналогично решаем и третье неравенство
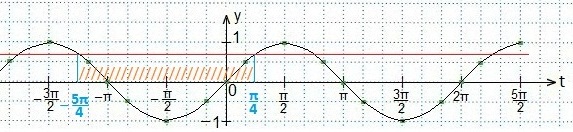
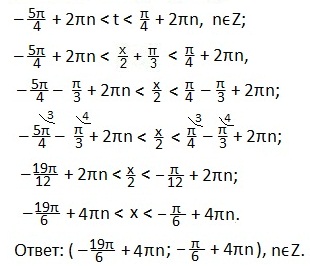В выделенном промежутке синусоида располагается ниже прямой, поэтому, учитывая периодичность функции синуса, запишем в виде двойного неравенства значения t. Затем вместо t подставим первоначальный аргумент синуса и будем выражать х из полученного двойного неравенства.
Ответ запишем в виде числового промежутка.
Смотрите видео: 10.2.1. Решение тригонометрических неравенств вида: sinx < a графическим способом.
И, напоследок: знаете ли вы, что математика — это определения, правила и ФОРМУЛЫ?!
Конечно, знаете! И самые любознательные, изучив эту статью и просмотрев видео, воскликнули: «Как долго и сложно! А нет ли формулы, позволяющей решать такие неравенства безо всяких графиков и окружностей?» Да, разумеется, есть!
ДЛЯ РЕШЕНИЯ НЕРАВЕНСТВ ВИДА: sint < a (-1≤а≤1) справедлива формула:
— π — arcsin a + 2πn < t < arcsin a + 2πn, nєZ.
Примените ее к рассмотренным примерам и вы получите ответ гораздо быстрее!
Вывод: УЧИТЕ ФОРМУЛЫ, ДРУЗЬЯ!
