Решить 2.7/2.9-1.1

На чтение 1 мин. Просмотров 10.8k.

Решаем пример с десятичными числами и дробями. Повторяем важные правила.

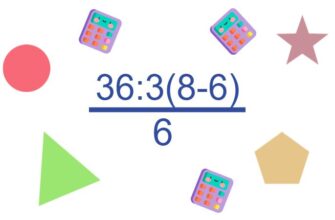
Задание на знание действий с десятичными дробями и с дробями вообще: решить $\displaystyle \frac{2,7}{2,9-1,1}$

Решение

Посчитаем значение выражения в знаменателе дроби: $\displaystyle 2,9-1,1=1,8$

Таким образом, у нас получается:

$\displaystyle \frac{2,7}{1,8}$

Теперь умножим числитель и знаменатель дроби на 10.

Нажми, чтобы узнать правило, по которому мы можем умножать дробь на 10

Дробь не изменится если числитель и знаменатель умножить на одно и то же число

\displaystyle  \frac{a}{b}=\frac{a \cdot k}{b \cdot k}

Получаем:

$\displaystyle \frac{2,7}{1,8}=\frac{27}{18}$

Теперь разделим числитель и знаменатель на 9.

$\displaystyle \frac{2,7}{1,8}=\frac{27}{18}=\frac{3}{2}=1,5$

Ответ: 1,5

Почему нам понадобилось умножать десятичную дробь на 10 и в числителе, и в знаменателе? Потому что гораздо проще работать с обычными числами, чем с десятичными. Чаще всего ошибки допускаются именно тогда когда умножают или делят десятичные числа. Эти ошибки касаются того, где именно стоит запятая, однако, и в вычислениях они случаются. Совет — если можно привести десятичное число к обычному, то лучше это сделать.