Решите неравенство t^2 \le 5t
Решение:
Перенесем все в левую часть:
t^2 -5t \le 0
Вынесем t за скобки:
t (t -5) \le 0
Решать будем методом интервалов, поэтому неравенство сделаем равенством и найдем корни полученного уравнения. При переходе через эти точки знак выражения слева от знака неравенства будет меняться.
t (t -5) = 0
t=0 или t -5 = 0
Получаем два корня:
t_1=0 или t_2 = 5
Это те точки, в которых мы имеем ноль.
При переходе через эти точки будет меняться знак. Поэтому отметим эти точки на числовой оси. Эти точки разделят всю числовую ось на три интервала.
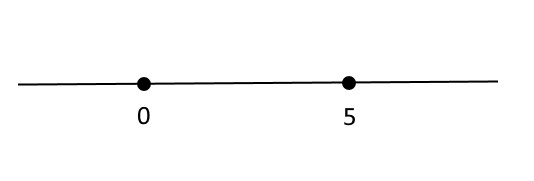
Найдем знак выражения t^2 -5t в полученных интервалах.
Для этого возьмем любое число из каждого промежутка и подставим в данное выражение, полученное значение выражения будет либо положительным, либо отрицательным. Если положительным — то на всем интервале будет «+», если отрицательным, то «-».
- Интервал (-\infty; 0] — возьмем число -1, и подставим в выражение t^2 -5t , получим: (-1)^2 -5 \cdot (-1) =1+5=6 . Значит, на данном интервале будет «плюс». Это означает, что все числа из данного промежутка, если их подставить в выражение t^2 -5t дадут только положительные значения.
- Интервал [0; 5]. Возьмем число 1 (всегда выбирайте такие числа, с которыми легче посчитать значение выражения). Подставляем 1^2 -5 \cdot 1 =1-5=-4 .
- Интервал [5; \infty). Возьмем число 6. Получаем: 6^2 -5 \cdot 6 =36-30=6 . Значение положительное.
Итак, мы проверили все интервалы, и отмечаем:
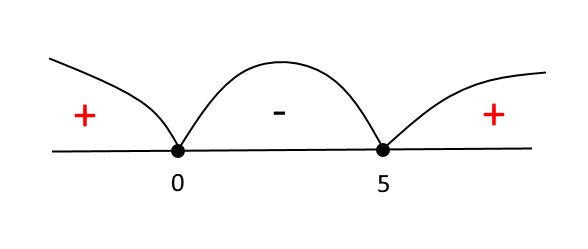
В исходном неравенстве мы должны найти все значения переменной, при которых выражение меньше, либо равно нулю. Этому условию удовлетворяют все числа внутри интервала, отмеченного нами знаком «-». Это и будет решение.
Ответ: [0; 5]
Данное неравенство можно также решить и графически — очевидно что слева у нас квадратичная функция, которая дает нам график — параболу. Точки 0 и 5 — это абсциссы, в которых график пересекает ось Ot. Посмотрите — как все наглядно видно на графике:
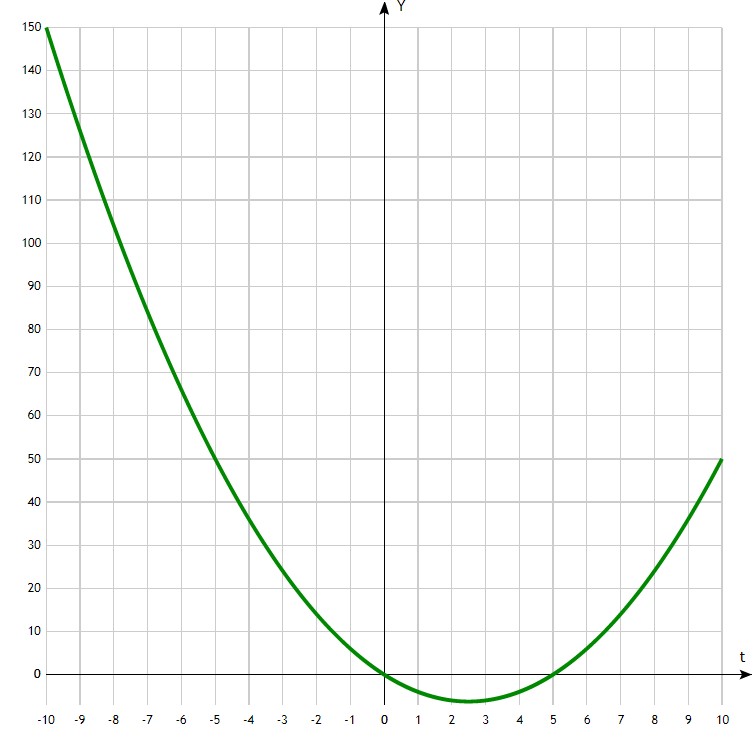
На графике видно, что в точках 0 и 5 он пересекает ось абсцисс, и все значения внутри области [0; 5] будут отрицательными.