В курсе алгебры 8 класса изучается теорема Виета. Основное применение этой теоремы — упрощение вычисления корней приведенного квадратного уравнения.
Приведенное квадратное уравнение — это квадратное уравнение, вида ![]() , где коэффициент
, где коэффициент ![]() равен единице. В случае такого уравнения или приведения к нему можно использовать теорему Виета. Обычно приведенное квадратное уравнение имеет вид:
равен единице. В случае такого уравнения или приведения к нему можно использовать теорему Виета. Обычно приведенное квадратное уравнение имеет вид: ![]() , где
, где ![]() ;
; ![]() . Любое квадратное уравнение можно привести к приведенному виду.
. Любое квадратное уравнение можно привести к приведенному виду.
В этой статье мы дадим определение теоремы Виета, докажем ее, покажем применение теоремы при решении квадратных уравнений, а также рассмотрим теорему обратную теореме Виета.
Содержание
Квадратное уравнение и его корни
Давайте вспомним, как решается обычное квадратное уравнение. Сначала мы определяем его дискриминант по формуле: ![]() , затем мы сравниваем дискриминант с нулем:
, затем мы сравниваем дискриминант с нулем:
- Если
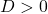 , то уравнение имеет два разных корня, которые определяются по формулам:
, то уравнение имеет два разных корня, которые определяются по формулам: 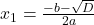 и
и 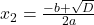
- Если
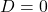 , то имеем два, совпадающих друг с другом корня:
, то имеем два, совпадающих друг с другом корня: 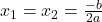 .
. - Если
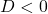 , то уравнение не имеет действительных корней.
, то уравнение не имеет действительных корней.
Давайте запишем уравнение и решим его.
![]()
Разделим левую и правую части на 2, получим приведенное квадратное уравнение:
![]()
Определим дискриминант: ![]() . Дискриминант больше нуля, значит, решением будут два корня:
. Дискриминант больше нуля, значит, решением будут два корня:
![]() и
и ![]() .
.
Сумма этих корней ![]() , а произведение
, а произведение ![]() . То есть сумма этих корней равна второму коэффициенту приведенного уравнения, взятому с противоположным знаком, а произведение равно свободному члену.
. То есть сумма этих корней равна второму коэффициенту приведенного уравнения, взятому с противоположным знаком, а произведение равно свободному члену.
Проанализировав множество приведенных уравнений и сумм и произведений их корней, французский математик Франсуа Виет (1540—1603) открыл эту закономерность и доказал, что она справедлива для всех приведенных уравнений. Эту закономерность он назвал теоремой, которую мы теперь знаем, как теорему Виета. Она была доказана в 1591 году.

Теорема Виета и ее доказательство
Теорема. Если ![]() и
и ![]() корни уравнения
корни уравнения ![]() , то
, то ![]() , а
, а ![]() .
.
Доказательство:
Используя формулу корней приведенного квадратного уравнения, запишем их сумму и произведение:
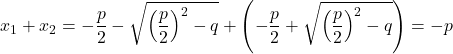
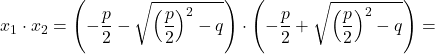
![]()
Что и требовалось доказать.
Квадратное уравнение, как уже говорилось выше, вида ![]() можно преобразовать к приведенному
можно преобразовать к приведенному ![]() и тогда корни по теореме Виета будут удовлетворять системе:
и тогда корни по теореме Виета будут удовлетворять системе:
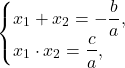
Теорема (обратная теореме Виета)
Если числа ![]() и
и ![]() такие, что их сумма равна
такие, что их сумма равна ![]() , а их произведение равно
, а их произведение равно ![]() , то они являются корнями уравнения
, то они являются корнями уравнения ![]() .
.
Доказательство.
Если ![]() , а
, а ![]() , то заменим
, то заменим ![]() и
и ![]() в уравнении:
в уравнении:
![]()
Если ![]() ,
, ![]() — корни уравнения, то, подставив в уравнение
— корни уравнения, то, подставив в уравнение ![]() сначала
сначала ![]() , потом
, потом ![]() , мы должны получить верное равенство.
, мы должны получить верное равенство.
![]()
![]()
![]()
То есть, мы доказали, что ![]() — корень уравнения.
— корень уравнения.
Подставим теперь ![]() :
:
![]()
![]()
![]()
Итак, доказано, что ![]() — корень уравнения
— корень уравнения ![]() .
.
Теорема доказана.
Примеры применения теоремы Виета
Рассмотрим примеры, в которых целесообразно применение теоремы Виета.
Пример 1
Напишите приведенное квадратное уравнение, корнями которого являются числа 25 и 2.
Решение:
Приведенное квадратное уравнение имеет вид:
![]()
По теореме Виета имеем:
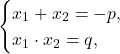
Тогда:
![]()
![]()
Искомое уравнение будет иметь вид:
![]()
Ответ: ![]() .
.
Пример 2
Решите уравнение, применяя теорему Виета.
![]()
Решение:
По теореме корни уравнения удовлетворяют системе:
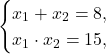
Подбирая, получим:
![]() ,
, ![]() .
.
Действительно, подставим данные корни по очереди в исходное уравнение, и проверим правильность решения.
![]()
![]()
![]()
![]()
![]()
![]()
Корни уравнения найдены верно.
Ответ: ![]() ,
, ![]() .
.
Пример 3
Требуется найти корни уравнения ![]() .
.
Решение:
Решать будем через теорему Виета, так как уравнение приведенное — старший коэффициент ![]() .
.
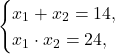 .
.
Корнями уравнения будут числа ![]() и
и ![]() . Они удовлетворяют системе. Сделаем проверку:
. Они удовлетворяют системе. Сделаем проверку:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ: ![]() и
и ![]() .
.
Совет 1. Если вы делаете выбор в пользу применения теоремы Виета, то обязательно делайте проверку, так как на этапе подбора корней очень часто совершаются ошибки.
Совет 2. Если вы не можете подобрать корни, используя теорему Виета, то вы всегда можете решить уравнение, используя формулы для корней квадратного уравнения.
Пример 4
Найдите сумму и произведение корней уравнения:
![]()
Решение:
Сумму и произведение корней найдем по формулам Виета ![]() ,
, ![]() .
.
Ответ: ![]() ,
, ![]() .
.
Пример 5
Составьте квадратное уравнение, корнями которого являются числа ![]() и
и ![]() .
.
Решение:
Связь между корнями уравнения и его коэффициентами устанавливает теорема Виета.
![]() , тогда
, тогда ![]() .
.
Определим ![]() :
:
![]()
Тогда уравнение будет иметь вид: ![]() .
.
Ответ: ![]() .
.
Согласно теореме Виета мы можем решить любое приведенное квадратное уравнение, которое имеет действительные корни. Соотношения Виета значительно упрощают решение квадратных уравнений, однако, если есть сложности с подбором корней, то всегда можно найти корни по общим формулам. Однако, применение теоремы Виета в случае, где она применима, считается наиболее рациональным путем решения.




Отлично объяснено. Спасибо.
Спасибо.