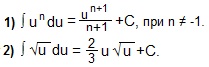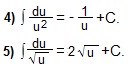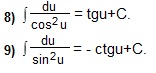Прежде, чем решать примеры на нахождение неопределенных интегралов, вспомним основные свойства и основные формулы неопределенных интегралов и запишем все это на отдельном листе "Интегралы".
Интегралы.
Основные свойства
I. (∫f (x) dx)'=f (x).
II. d∫f (x) dx=f (x) dx.
III. ∫dF (x)=F (x)+C или ∫F'(x) dx=F (x)+C.
IV. ∫kf (x) dx=k·∫f (x) dx, где k - постоянная величина, не равная нулю.
V. ∫(f (x)±g (x)) dx=∫f (x) dx±∫g (x) dx.
VI. Если F (x) есть первообразная для f (x), а k и b - постоянные величины,
причем, k≠0, то (1/k)·F (kx+b) есть первообразная для f (kx+b).
Справедливо равенство:
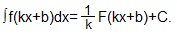
Даже простейшие примеры на нахождение неопределенных интегралов предполагают хорошее знание таблицы интегралов. С этого и начнем, причем, перепишем все формулы таблицы интегралов для функции u, которая зависит от х. Итак, мы будем считать, что u - не простая переменная, а функция от х, т.е. u=φ(x), тогда нижеприведенная таблица интегралов окажется справедливой в любом случае: и если переменная интегрирования является независимой переменной, и если переменная интегрирования есть функция от независимой переменной.
Таблица интегралов
3) ∫du=u+C.
6) ∫cosudu=sinu+C.
7) ∫sinudu=-cosu+C.
Примеры
Найти следующие интегралы и сделать проверку.
1) ∫(2x – 3) dx. Используем свойства V и IV, формулы 1). и 3).
(Наш лист Интегралы)
∫(2x – 3) dx = 2∫xdx - 3∫dx = 2·x²/2 – 3x + C = х2 – 3х + С.
Проверка. F'(x) = (х2 – 3х + С)' = 2x – 3 = f (x).
2). ∫(2x – 3)2dx. Преобразуем подынтегральную функцию по формуле ФСУ (формулы сокращенного умножения): (a – b)2 = a2 – 2ab + b2, а затем используем те же свойства и формулы, что и в примере 1).
∫(2x – 3)2dx =∫( 4x2 – 12x + 9) dx = 4∫x2dx — 12∫xdx + 9∫dx =
= 4·x³/3 — 12· x²/2 + 9x + C = ( 4/3) x3 – 6x2 + 9x + C.
Проверка. F'(x) = ((4/3) x3 – 6x2 + 9x + C)' =(4/3) · 3x2 — 6·2x + 9 = 4x2 – 12x + 9 = (2x – 3)2 = f (x).
Решим пример 2) вторым способом - подведения под знак дифференциала.
Итак, требуется найти ∫(2x – 3)2dx.
Будем использовать формулу 1). Вместо u у нас (2х – 3) и, по формуле 1), переменная интегрирования должна быть такой же, как и основание степени, т. е (2х – 3). Хорошо, вместо dx запишем d(2x – 3). И что изменилось? d (2x – 3) = 2dx, т.е. подынтегральное выражение стало больше в 2 раза. Разделим его на 2. Для этого перед значком интеграла поставим множитель ½.
Значит,∫(2x – 3)2dx = (½)∫( 2x – 3)2 d (2x – 3). Мысленно представляйте себе u2 вместо
(2х – 3)2 и du вместо d(2x – 3). Увидели ∫u2du ? И что получится? Верно: u³/3+ C.
«Долго сказка сказывается…», а решаются такие примеры быстро:
∫(2x – 3)2dx = (½)∫(2x – 3)2 d (2x – 3) =(½) ·(2x-3)³/3 + С =(1/6) · (2х – 3)3 + С.
Проверка. (F (x)+С)′ = ( 1/6· (2х – 3)3 + С)' = (1/6)· 3 (2x – 3)2 · 2 = (2x – 3)2 = f (x).
Сравните эти два способа решения примера 2. Что, не впечатлил второй способ? Тогда пример 3).
3) ∫(2x – 3)7dx. Желаете возводить (2х – 3) в седьмую степень? А-а, то-то же!
Решаем способом подведения под знак дифференциала, т.е. вторым способом так же, как предыдущий пример.
∫(2x – 3)7dx = (½)∫(2x – 3)7d (2x – 3) = (½)· (2x – 3)8 /8 + C =(1/16) (2x – 3)8 + C.
Проверка. F'(x) = ((1/16)(2x – 3)8 + C)' =(1/16) ·8 (2x – 3)7·2 = (2x – 3)7 = f (x).