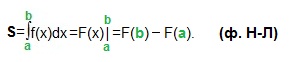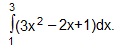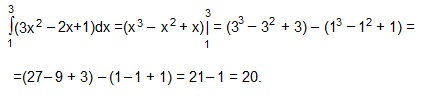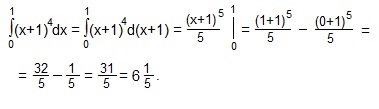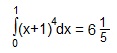Пора познакомиться с мощнейшим средством исследования в математике, физике, механике и других точных дисциплинах. Это средство — определенный интеграл. В средней школе определенный интеграл применяют при вычислениях площадей криволинейных трапеций, объемов тел вращения, нахождении моментов инерции и т.д.
Что такое определенный интеграл? Чем он отличается от неопределенного, с которым мы уже достаточно знакомы.
Сравните:
a и b — это границы, в которых изменяется переменная интегрирования х.
Сравниваем далее:
Неопределенный интеграл графически представляет собой семейство кривых, совмещаемых параллельным переносом (11.1.9).
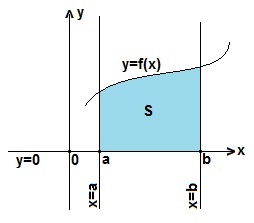Определенный интеграл (см. рисунок слева) представляет собой криволинейную трапецию, ограниченную сверху графиком функции y=f (x), снизу — осью Ох, а слева и справа прямыми x=a и х=b.
Значение определенного интеграла есть площадь S этой криволинейной трапеции:
Рассмотрим примеры на вычисление определенного интеграла.
Пример 1.
Найдем первообразную F (x) для подынтегральной функции f (x)=3x²-2x+1, а затем применим формулу Ньютона-Лейбница (ф. Н-Л).
Пример 2.
Возникает вопрос: раз определенный интеграл выражает собой площадь криволинейной трапеции, то нельзя ли увидеть эту криволинейную трапецию? А можно! Проиллюстрируем пример 2.
Полученный результат
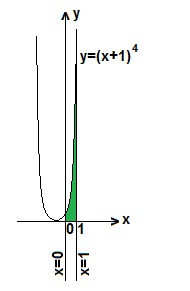выражает площадь криволинейной трапеции, ограниченной графиком функции y=(x+1)4, осью Ох и прямыми: х=0 (осью Оy) и х=1.
График функции y=(x+1)4 - парабола, ветви которой направлены вверх,
а вершина находится в точке О′(-1; 0).
Площадь этой криволинейной трапеции:
