Вспомним определения:
1. Дифференцируемая функция F (x) называется первообразной для функции f (x) на заданном промежутке, если для всех х из этого промежутка справедливо равенство:
F′(x)=f (x).
2. Совокупность всех первообразных F (x)+C функции f (x) на рассматриваемом промежутке называется неопределенным интегралом.
Как можно представить себе неопределенный интеграл
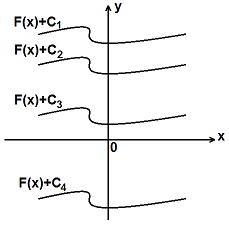где F (x) - первообразная функции f (x), а С - некоторая постоянная величина?
Если в данном примере или задаче не даются начальные условия для нахождения величины С, то мы получаем неоднозначную функцию F (x)+С - семейство интегральных кривых. Графики этих кривых можно совместить с помощью параллельного переноса. Из семейства этих кривых нам нужно уметь выделять ту, которая проходит через данную точку.
Пример 1
Найти для функции f (x)=1-2x первообразную, график которой проходит через точку М(3; 2).
Решение.
F (x)=∫(1-2x) dx=∫dx-2∫xdx=x-x²+C.
Так как F (3)=2 по условию, то получаем равенство:
2=3-3²+С;
2=3-9+С;
2=-6+С → С=8.
Тогда F (x)=x-x²+8.
Пример 2
Найти ∫(sinx-cosx) dx, если при π/2 первообразная равна 6.
Решение.
∫(sinx-cosx) dx=∫sinxdx-∫cosxdx=-cosx-sinx+C.
По условию F (π/2)=6. Получаем равенство: -cos (π/2) -sin (π/2)+C=6;
0-1+C=6 → C=6+1; C=7.
Искомая функция F (x)=-cosx-sinx+7.
Пример 3
Найти первообразную для функции
принимает значение, равное нулю.
Решение.
