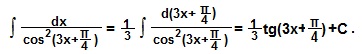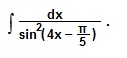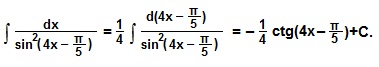Содержание
Пример 1
∫sin3xdx.
У нас есть формула 7). Интегралы: ∫sinudu= — cos u + C.
Из этой формулы следует, что какой аргумент у синуса – такой же должна быть и переменная интегрирования. Будем считать, что в нашем случае u = 3x, тогда du = 3dx. Подведем под знак дифференциала 3х, не забыв уравнять обе части равенства.
∫sin3xdx=(1/3)∫sin3xd (3x) = — (1/3) cos 3x + C.
Проверка.
(F (x)+C)' = ( — 1/3 cos 3x + C)' = — (1/3) · (cos 3x)' = — (1/3) · (-3sin 3x) = sin 3x = f (x).
Пример 2
∫cos (4x+3) dx.
Используем формулу 6). Интегралы: ∫cosudu=sinu+C.
Подводим под знак дифференциала (4х + 3). Так как d (4x + 3) = 4dx, то
∫cos (4x+3) dx=(¼)∫cos (4x+3) d (4x+3) =(¼) sin (4x + 3) + C.
Проверка.
(F (x)+C)'= ( (¼) sin (4x + 3) + C)' = (¼) · 4 cos (4x + 3) = cos (4x + 3) = f (x).
Пример 3
Какую формулу напоминает этот пример? Правильно, формулу 8). Интегралы.
Подводим под знак дифференциала (3х+π/4). Тогда d (3x+π/4) = 3dx, значит, чтобы значение данного выражения не изменилось, поставим перед знаком интеграла 1/3.
Пример 4
Чтобы применить формулу 9). Интегралы, нужно подвести под знак дифференциала (4х- π/5). Отсюда следует: d (4х-π/5)=4dx. Перед знаком интеграла поставим множитель ¼.