Показательная функция — одна из основных функций, изучаемая в школе и в ВУЗе. Познакомимся с основными понятиями и свойствами показательной функции, построим ее график.
- Функцию вида y=ax, где а > 0, a≠1, х – любое число, называют показательной функцией.
- Область определения показательной функции: D (y)=R – множество всех действительных чисел.
- Область значений показательной функции: E (y)=R+ - множество всех положительных чисел.
- Показательная функция y=ax возрастает при a > 1.
- Показательная функция y=ax убывает при 0 < a < 1.
Справедливы все свойства степенной функции:
- а0=1 Любое число (кроме нуля) в нулевой степени равно единице.
- а1=а Любое число в первой степени равно самому себе.
- ax∙ay=ax+y При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
- ax:ay=ax- y При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
- (ax)y=axy При возведении степени в степень основание оставляют прежним, а показатели перемножают
- (a∙b)x=ax∙by При возведении произведения в степень возводят в эту степень каждый из множителей.
- (a/b)x=ax/by При возведении дроби в степень возводят в эту степень и числитель и знаменатель дроби.
- а-х=1/ax
- (a/b)-x=(b/a)x.
Рассмотрим несколько примеров.
Содержание
Пример 1
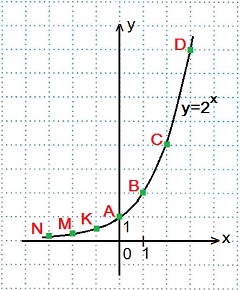
1) Построить график функции y=2x. Найдем значения функции
при х=0, х=±1, х=±2, х=±3.
x=0, y=20=1; Точка А.
x=1, y=21=2; Точка В.
x=2, y=22=4; Точка С.
x=3, y=23=8; Точка D.
x=-1, y=2-1=1/2=0,5; Точка K.
x=-2, y=2-2=1/4=0,25; Точка M.
x=-3, y=2-3=1/8=0,125; Точка N.
Большему значению аргумента х соответствует и большее значение функции у. Функция y=2x возрастает на всей области определения D (y)=R, так как основание функции 2 > 1.
Пример 2
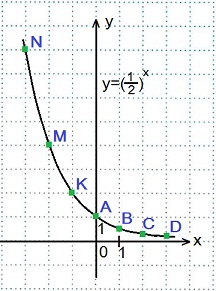
2) Построить график функции y=(1/2)x. Найдем значения функции
при х=0, х=±1, х=±2, х=±3.
x=0, y=(½)0=1; Точка A.
x=1, y=(½)1=½=0,5; Точка B.
x=2, y=(½)2=¼=0,25; Точка C.
x=3, y=(½)3=1/8=0,125; Точка D.
x=-1, y=(½)-1=21=2; Точка K.
x=-2, y=(½)-2=22=4; Точка M.
x=-3, y=(½)-3=23=8; Точка N.
Большему значению аргумента х соответствует меньшее значение функции y. Функция y=(1/2)x убывает на всей своей области определения: D (y)=R, так как основание функции 0 < (1/2) < 1.
Пример 3
3) В одной координатной плоскости построить графики функций:
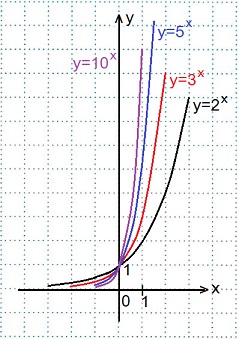
y=2x, y=3x, y=5x, y=10x. Сделать выводы.
График функции у=2х мы уже строили, графики остальных функций строим аналогично, причем, достаточно будет найти значения функций при х=0 и при х=±1.
Переменная х может принимать любое значение (D (y)=R), при этом значение у всегда будет больше нуля (E (y)=R+).
Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю. Чем больше основание а (если a > 1) показательной функции у=ах, тем ближе расположена кривая к оси Оу.
Все данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.
Пример 4
4) В одной координатной плоскости построить графики функций:
y=(1/2)x, y=(1/3)x, y=(1/5)x, y=(1/10)x. Сделать выводы.
Смотрите построение графика функции y=(1/2)x выше, графики остальных функций строим аналогично, вычислив их значения при х=0 и при х=±1.
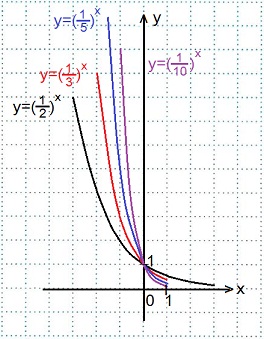Переменная х может принимать любое значение: D (y)=R, при этом область значений функции: E (y)=R+.
Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю.
Чем меньше основание а (при 0 < a < 1) показательной функции у=ах, тем ближе расположена кривая к оси Оу.
Все эти функции являются убывающими, так как большему значению аргумента соответствует меньшее значение функции.
Решить графически уравнения:
1) 3x=4-x.
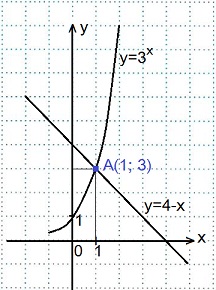В одной координатной плоскости построим графики функций: у=3х и у=4-х.
Графики пересеклись в точке А(1; 3).
Ответ: 1.
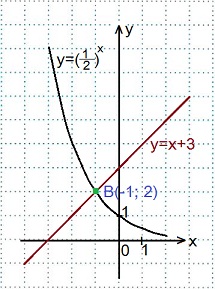
2) 0,5х=х+3.
В одной координатной плоскости строим графики функций: у=0,5х
(y=(1/2)x )
и у=х+3.
Графики пересеклись в точке В(-1; 2).
Ответ: -1.
Найти область значений функции: 1) y=-2x; 2) y=(1/3)x+1; 3) y=3x+1-5.
Решение.
1) y=-2x
Область значений показательной функции y=2x – все положительные числа, т.е.
0 < 2x < +∞. Значит, умножая каждую часть двойного неравенства на (-1), получаем:
— ∞ < -2x < 0.
Ответ: Е(у)=(-∞; 0).
2) y=(1/3)x+1;
0 < (1/3)x < +∞, тогда, прибавляя ко всем частям двойного неравенства число 1, получаем:
0+1 < (1/3)x+1 < +∞+1;
1 < (1/3)x+1 < +∞.
Ответ: Е(у)=(1; +∞).
3) y=3x+1-5.
Запишем функцию в виде: у=3х∙3-5.
0 < 3x < +∞; умножаем все части двойного неравенства на 3:
0∙3 < 3x∙3 < (+∞)∙3;
0 < 3x∙3 < +∞; из всех частей двойного неравенства вычитаем 5:
0-5 < 3x∙3-5 < +∞-5;
— 5 < 3x∙3-5 < +∞.
Ответ: Е(у)=(-5; +∞).
