11.3.3. Решение простейших показательных неравенств

Простейшими считаются показательные неравенства вида: a^x < a^y, a^x > a^y.  (a^x≤a^y, a^x≥a^y).

Так же, как и при решении простейших показательных уравнений, одинаковые основания степеней опускают, но знак нового неравенства сохраняют, если функция у=а^х является возрастающей (а > 1); eсли же показательная функция у=а^х убывает (0 < a < 1), то знак нового неравенства меняют на противоположный:

a^x < a^y → x < y, если a > 1; знак сохранен, так как функция возрастает;

a^x < a^y → x > y,  если 0 < a < 1; функция убывает – знак поменялся;

a^x > a^y → x > y, если  a > 1; знак сохранен, так как функция возрастает

a^x > a^y → x < y, если 0 < a < 1; функция убывает – знак поменялся.

Рассмотрим несколько примеров.

Решить неравенство:

Пример 1

1) 4^5-2x < 0,25.

Представим правую часть в виде: 0,25=(²⁵/₁₀₀)=(¹/₄)=4^-1;

4^5-2x < 4^-1; функция у=4^х с основанием 4 > 1 возрастает на R, поэтому, опуская основания степеней, знак неравенства сохраним:

5-2x < -1;

— 2x < -1-5;

— 2x < -6  |:(-2) при делении обеих частей неравенства на отрицательное число, знак неравенства меняют на противоположный:

x > 3.

Ответ: (3; +∞).

Пример 2

2) 0,4^2х+1≥0,16.

Представим число 0,16 в виде степени числа 0,4. Получаем:

0,4^2х+1≥0,4²; основание степеней – число 0,4 — удовлетворяет условию: 0 < 0,4 < 1; поэтому, опускаем основания степеней, а знак неравенства меняем на противоположный:

2х+1≤2;

2х≤2-1;

2х≤1  |:2

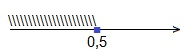
x≤0,5.

Ответ: (-∞; 0,5].

Пример 3

3) 2^3-x+2^1-x > 40.  Применим формулу: a^x+y=a^x∙a^y.  Запишем неравенство в виде:

2³∙2^-x+2¹∙2^-x > 40; Вынесем общий множитель за скобки:

2^-x∙(2³+2¹) > 40;   упрощаем левую часть:

2^-x∙(8+2) > 40;

2^-x∙10 > 40   |:10

2^-x > 4;

2^-x > 2²;  основание степени — число 2 > 1, значит, знак неравенства сохраняем:

— x > 2  |:(-1) при делении обеих частей неравенства на отрицательное число — знак неравенства меняют на противоположный:

x < -2.

Ответ: (-∞; -2).

Пример 4

4) 3^x+2+3^x+1+3^x≤39. Применяем формулу:  a^x∙a^y=a^x+y

3^x∙3²+3^x∙3¹+3^x≤39; вынесем общий множитель за скобки:

3^x∙(3²+3¹+1)≤39; упрощаем левую часть неравенства:

3^x∙(9+3+1)≤39;

3^x∙13≤39  |:13

3^x≤3;

3^x≤3¹; Показательная функция с основанием 3 (3 > 1) является возрастающей, поэтому, знак неравенства сохраним:

x≤1.

Ответ: (-∞; 1].