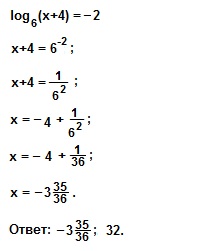11.4.1. Определение логарифма

Логарифмом числа b по основанию а (log_ab)  называют показатель степени, в которую нужно  возвести число а, чтобы получить число b.

log_ab=n, если aⁿ=b. Примеры: 1) log₂8=3, т. к. 2³=8;

2) log₅(1/25)=-2, т. к. 5^-2=1/5²=1/25;                         3) log₇1=0, т. к. 7⁰=1.

 Вычислить:

1)    log₄64+log₅25.  Используем значения степеней: 4³=64, 5²=25 и определение логарифма.

log₄64+log₅25=3+2=5.

2)    log₂log₃81.        Используем значения степеней: 3⁴=81, 2²=4 и определение логарифма.

log₂log₃81=log₂4=2.

3)    log₅log₉log₂512.    Используем значения степеней: 2⁹=512, 5⁰=1 и определение логарифма.

log₅log₉log₂512=log₅log₉9=log₅1=0.

Примеры решения логарифмических уравнений

1)    log₇x=2.          По определению логарифма составим равенство: x=7², отсюда х=49.

2)    log₃(x-5)=2.

По определению логарифма:

х-5=3²;

х-5=9;

х=9+5;

х=14.

3)    |log₆(x+4)|=2.

Освободимся от знака модуля.

или  log₆(x+4) =2;

x+4=6²;

x+4=36;

x=36-4;

x=32.