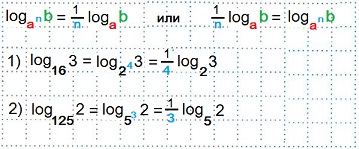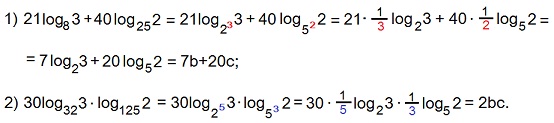11.4.9.3. Логарифм по основанию а, взятом в степени n

log_aⁿb=(1/n)∙log_ab     

Логарифм числа b по основанию aⁿ равен произведению дроби 1/n на логарифм числа b по основанию a.

 

Найти: 1) 21log₈3+40log₂₅2; 2) 30log₃₂3∙log₁₂₅2, если известно, что log₂3=b, log₅2=c.

Решение.

Ниже решим два уравнения.

Уравнение 1

1) log₂x+log₄x+log₁₆x=5,25.

Решение.

Приведем данные логарифмы к основанию 2.  Применим формулу: log_aⁿb=(1/n)∙log_ab     

log₂x+(½) log₂x+(¼) log₂x=5,25;

log₂x+0,5log₂x+0,25log₂x=5,25. Приводим подобные слагаемые:

(1+0,5+0,25)·log₂x=5,25;

1,75·log₂x=5,25  |:1,75

log₂x=3. По определению логарифма:

x=2³

x=8.

Ответ: 8.

Уравнение 2

2) 0,5log₄(x-2)+log₁₆(x-3)=0,25.

Решение.  Логарифм по основанию 16 приведем к основанию 4.

0,5log₄(x-2)+0,5log₄(x-3)=0,25 |:0,5

log₄(x-2)+log₄(x-3)=0,5. Преобразуем сумму логарифмов в логарифм произведения.

log₄((x-2)(x-3))=0,5;

log₄(x²-2x-3x+6)=0,5;

log₄(x²-5x+6)=0,5. По определению логарифма:

x²-5x+6=4^0,5

x²-5x+6=2;

x²-5x+4=0. По теореме Виета:

x₁=1; x₂=4. Первое значение х не подойдет, так как при х=1 логарифмы данного равенства не существуют, ведь под знаком логарифма могут находиться только положительные числа.

Проверим данное уравнение при х=4.

Проверка.

0,5log₄(4-2)+log₁₆(4-3)=0,25

0,5log₄2+log₁₆1=0,25

0,5∙0,5+0=0,25

0,25=0,25.

Ответ: 4.