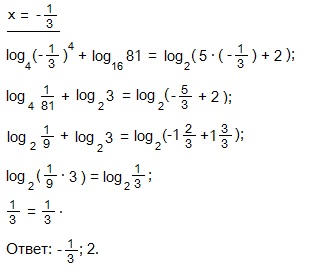logarbr=logabили logab=logarbr
Значение логарифма не изменится, если основание логарифма и число под знаком логарифма возвести в одну и ту же степень.
Под знаком логарифма могут находиться только положительные числа, причем, основание логарифма не равно единице.
Рассмотрим примеры.
Пример 1
1) Сравнить log39 и log981.
log39=2, так как 32=9;
log981=2, так как 92=81.
Значит, log39=log981.
Заметим, что основание второго логарифма равно квадрату основания первого логарифма: 9=32, а число под знаком второго логарифма равно квадрату числа под знаком первого логарифма: 81=92. Получается, что и число и основание первого логарифма log39 были возведены во вторую степень, и значение логарифма от этого не изменилось:
Далее, так как извлечение корня n-й степени из числа а есть возведение числа а в степень (1/n), то из log981 можно получить log39 извлечением квадратного корня из числа и из основания логарифма:
Пример 2
2) Проверить равенство: log425=log0,50,2.
Рассмотрим первый логарифм. Извлечем квадратный корень из основания 4 и из числа 25; получаем: log425=log25.
Рассмотрим второй логарифм. Основание логарифма: 0,5=1/2. Число под знаком этого логарифма: 0,2=1/5. Возведем каждое из этих чисел в минус первую степень:
0,5-1=(1/2)-1=2;
0,2-1=(1/5)-1=5.
Таким образом, log0,50,2=log25. Вывод: данное равенство верно.
Решить уравнение:
log4x4+log1681=log2(5x+2). Приведем логарифмы слева к основанию 2.
log2x2+log23=log2(5x+2). Извлекли квадратный корень из числа и из основания первого логарифма. Извлекли корень четвертой степени из числа и основания второго логарифма.
log2(3x2)=log2(5x+2). Преобразовали сумму логарифмов в логарифм произведения.
3x2=5x+2. Получили после потенцирования.
3x2-5x-2=0. Решаем квадратное уравнение по общей формуле для полного квадратного уравнения:
a=3, b=-5, c=-2.
D=b2-4ac=(-5)2-4∙3∙(-2)=25+24=49=72 > 0; 2 действительных корня.
Проверка.
log424+log1681=log2(5∙2+2);
log222+log23=log212;
log2(4∙3)=log212;
log212=log212;
12=12.