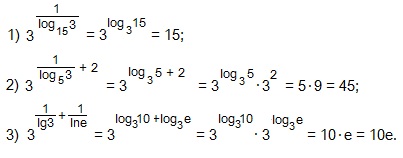11.4.9. Логарифмы. 1-я формула перехода к новому основанию

Основание логарифма и число под знаком логарифма можно поменять местами по формуле:

log_ab=1/log_ba   Логарифм числа b по основанию а равен единице, деленной на логарифм числа а по основанию b.

Пример: log₂₅5=1/log₅25.

Действительно, log₂₅5=½=0,5; так как 25^0,5=(5²)^0,5=5^2∙0,5=5¹=5.

log₅25=2, так как 5²=25.

Получаем верное равенство: 0,5=1/2.

Вычислить:

Давайте решим два уравнения.

Уравнение 1

1) 2log₂x+1/log_x2=9. Применяем формулу:  log_ab=1/log_ba.  Получаем:

2log₂x+log₂x=9, приводим подобные слагаемые:

3log₂x=9  |:3

log₂x=3, далее, по определению логарифма:

x=2³;

x=8.

Проверка.

Подставляем значение 8 вместо х в исходное уравнение.

2log₂8+1/log₈2=9;

2∙3+1/(1/3)=9;

6+3=9;  9=9.

Ответ: 8.

Уравнение 2

2) lg(x-2)+1/(log_(x+3)10)=lg6. Применяем формулу: log_ab=1/log_ba. Получаем:

lg (x-2)+lg (x+3)=lg6, используем формулу: log_ax+log_ay=log_a(x∙y);

lg ((x-2)∙(x+3))=lg6. Потенцируем:

(x-2)∙(x+3)=6, перемножаем двучлены:

x²-2x+3x-6=6, перенесем 6 из правой части в левую и приведем подобные слагаемые:

x²+x-12=0 – это приведенное квадратное уравнение.

x₁=-4, x₂=3, так как по теореме Виета сумма корней должна быть равна второму коэффициенту, взятому с противоположным знаком, т.е. числу -1 (-4+3=-1), а произведение должно быть равно свободному члену, т.е. числу -12 (-4∙3=-12).

Значение х=-4 не удовлетворяет условию существования логарифма (под знаком логарифма могут быть только положительные числа, причем основание логарифма не равно единице)

Сделаем проверку при х=3.

lg (3-2)+1/(log₍₃₊₃₎10)=lg6

lg1+1/log₆10=lg6

0+lg6=lg6;     lg6=lg6.

Ответ: 3.