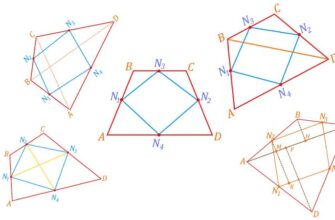
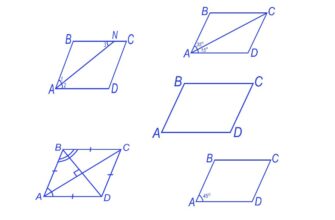
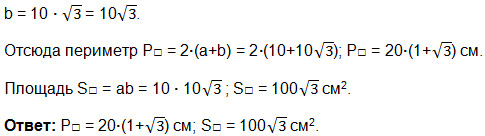Задача 1. Диагональ прямоугольника равна 16 и составляет со стороной угол 30°. Найти площадь прямоугольника.
Решение.
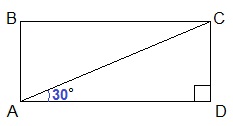1 способ. Площадь прямоугольника найдем по формуле: S = ab (площадь прямоугольника равна произведению его длины на ширину). Для этого нам нужно найти стороны прямоугольника. Рассмотрим прямоугольный ∆ADC, в котором искомые стороны прямоугольника AD и CD являются катетами. Гипотенуза АС=16, острый ∠САD=30°. Катет, лежащий против угла 30°, равен половине гипотенузы. Следовательно, CD=16:2=8. Второй катет AD найдем по теореме Пифагора: AD2+CD2=AC2. Подставляем значения. AD2+82=162; AD2+64=256; AD2=256-64; AD2=192;
Катет AD можно было найти иначе – через косинус ∠САD. Так как косинусом острого угла прямоугольного треугольника называется отношение прилежащего углу катета к гипотенузе, то отсюда следует: катет, прилежащий углу, равен произведению гипотенузы на косинус этого угла.
У нас: AD=AC∙cos30°;
Подставим найденные значения в формулу площади прямоугольника.
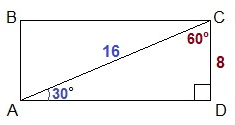2 способ. Пусть в прямоугольнике ABCD диагональ АС составляет угол 30° со стороной AD. Мы знаем, что диагональ прямоугольника делит прямоугольник на два равных треугольника. Рассмотрим один из этих треугольников – прямоугольный ∆ ADC (∠ADC=90°) CD – катет, противолежащий углу 30°, поэтому этот катет равен половине гипотенузы, т.е. CD = АС : 2 = 16 : 2 = 8 (см). Второй острый угол рассматриваемого прямоугольного ∆ ADC – угол AСD равен 60° (90°-30°=60°). Площадь треугольника ADC равна половине произведения двух его сторон АС и CD на синус угла между ними. Тогда площадь прямоугольника равна произведению АС и CD на синус угла между ними:
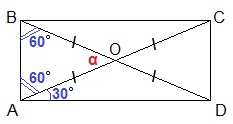3 способ основан на том, что площадь прямоугольника можно найти как половину произведения его диагоналей на синус угла между ними. Проведем вторую диагональ BD и обозначим точку пересечения диагоналей через О. Углом между двумя пересекающимися прямыми считают меньший из образовавшихся углов. У нас это угол АОВ. Обозначим его через α. Найдем градусную меру угла α. Так как диагонали прямоугольника равны и точкой пересечения делятся пополам, то ∆АОВ – равнобедренный с углами при основании по 60°. На самом деле: ∠ОАВ=90°-∠САD=90°-30°=60°. Третий угол треугольника АОВ, т.е. угол α также равен 60° (считали: 180°-60°-60°). Площадь прямоугольника:
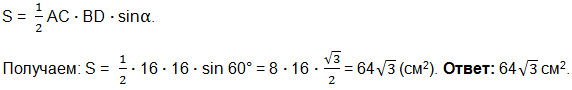
Задача 2. Диагональ прямоугольника составляет с его стороной, равной 10 см, угол 60°. Найти периметр и площадь прямоугольника.
Решение.
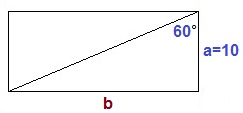Периметр прямоугольника P□ = 2 (a+b), S□ = ab, где a и b – стороны прямоугольника. Нам известна лишь одна сторона: а = 10. Найдем вторую сторону, как неизвестный катет прямоугольного треугольника, противолежащий углу 60°. Так как тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему, то b = a ∙ tg60°. Подставляем значения и получаем:
