Задача 1. Одна сторона прямоугольника меньше другой на 7 см, а диагональ прямоугольника равна 17 см. Найти периметр прямоугольника.
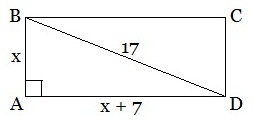Решение. Пусть АВ=х. Тогда AD=х+7. Зная, что диагональ BD=17, используем теорему Пифагора и составим уравнение:
AB2 +AD2=BD2. Получаем: х2+(х+7)2=172 ⇒ х2+х2+14х+49=289;
2х2+14х-240=0; х2+7х-120=0, отсюда по теореме Виета х1=-15; х2=8.
Следовательно, АВ=8 см, AD=8+7=15 см. Периметр прямоугольника:
P□ = 2∙(AB+AD); P□ = 2∙(8+15); P□ = 46 см. Ответ: 46 см.
Задача 2. Периметр прямоугольника 94 см, а диагональ 37 см. Найти площадь прямоугольника.
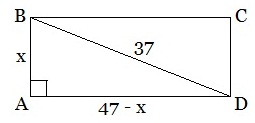Решение. Периметр прямоугольника P□ = 2∙(AB+AD) = 94, следовательно, (AB+AD)=47. Пусть АВ=х. Тогда AD=47-х. Зная, что диагональ BD=37, используем теорему Пифагора и составим уравнение:
AB2 +AD2=BD2. Получаем: х2+(47-х)2=372 ⇒ х2+472-94х+ х2=1369;
2х2-94х+2209—1369=0; 2х2-94х+840=0. Делим обе части равенства на 2. Получаем:
х2-47х+420=0. Найдем дискриминант.
D=b2-4ac=472-4∙1∙420=2209—1680=529=232>0; 2 д.к.
х1 = (47-23)/2=12; х2 = (47+23)/2=35.
Так как АВ=х, то либо АВ=12, тогда AD=47-12=35; либо АВ=35, тогда AD=47-35=12. Таким образом, стороны прямоугольника равны 12 см и 35 см. Площадь прямоугольника S□ = AB∙AD=12∙35=420 (см2). Ответ: 420 см2.
Задача 3. Стороны прямоугольника относятся как 3:4, а площадь прямоугольника равна 108 см2. Найти диагональ прямоугольника.
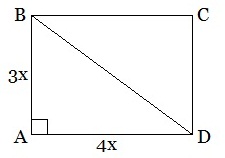Решение. Обозначим одну часть через х. Тогда АВ=3х. Тогда AD=4х.
Так как S□ = AB∙AD и по условию равна 108 см2, то можно составить уравнение:
3х∙4х=108. Тогда 12х2=108, а разделив обе части равенства на 12, получаем:
х2=9. Отсюда х=3, так как х – положительное число. Стороны прямоугольника
Тогда АВ=3х=3∙3=9 и AD=4х=4∙3=12. Из прямоугольного треугольника BAD по теореме Пифагора найдем BD – искомую диагональ прямоугольника.
BD2=AB2+AD2=92+122=81+144=225, отсюда BD=15 см. Ответ: 15 см.
Задача 4. Биссектриса одного из углов прямоугольника делит сторону прямоугольника пополам. Найдите диагональ прямоугольника, если его меньшая сторона равна 15 см.
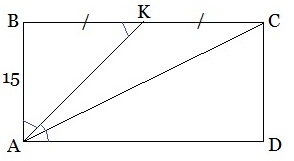Решение. Итак, в прямоугольнике ABCD биссектриса АК делит сторону ВС пополам. АВ=15 см. Требуется найти диагональ АС прямоугольника. В прямоугольном треугольнике АВК один из острых углов равен 45° (биссектриса АК делит прямой угол пополам: ∠ВАК=∠КАD=45°). Тогда и второй острый угол треугольника АВК равен 45°, т.е. ∠АКВ=45°. Углы при основании ∆АВК равны, следовательно, ∆АВК – равнобедренный. Это означает, что ВК=АВ=15 см. А так как биссектриса АК по условию разделила сторону ВС пополам, то ВС=2∙ВК=30 см. Стороны прямоугольника 15 см и 30 см. Из прямоугольного треугольника АВС по теореме Пифагора найдем АС – искомую диагональ прямоугольника.
АС2=AB2+ВС2=152+302=225+900=1125, отсюда получаем:
Задача 5. В прямоугольнике точка пересечения диагоналей отстоит от меньшей стороны на 7 см дальше, чем от большей стороны. Диагональ прямоугольника равна 26 см. Найдите стороны прямоугольника.
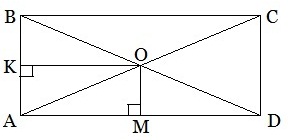Решение. Пусть точка О – пересечение диагоналей прямоугольника ABCD отстоит от стороны AD на х см, тогда от стороны АВ точка О будет отстоять на (х+7) см, т.е ОМ=х и ОК=х+7. Так как диагонали прямоугольника равны и точкой пересечения делятся пополам, то АО=АС:2=26:2=13 (см). Заметим, что МА=ОК. На основании теоремы Пифагора из прямоугольного треугольника АМО получаем равенство:
ОМ2+МА2=АО2 или х2+(х+7)2=132. Упрощаем равенство:
х2+х2+14х+49=169; 2х2+14х-120=0; х2+7х-60=0. Корни этого приведенного квадратного уравнения удобно найти по теореме Виета.
х1=-12, х2=5. Так как сторона выражается положительным числом, то ОМ=х=5 см. тогда ОК=5+7=12 (см). АК=ОМ=5 см и АМ=ОК=12 см – это половинки сторон прямоугольника. Тогда АВ=2∙АК=10 см и AD=2∙МА=24 см. Ответ: 10 см и 24 см.
