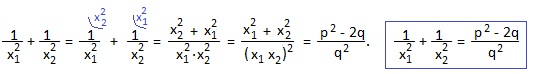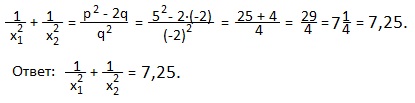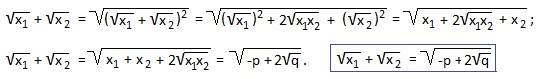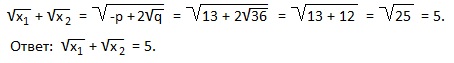Часто требуется найти сумму квадратов (x12+x22) или сумму кубов (x13+x23) корней квадратного уравнения, реже — сумму обратных значений квадратов корней или сумму арифметических квадратных корней из корней квадратного уравнения:
Помочь в этом может теорема Виета:
Сумма корней приведенного квадратного уравнения x2+px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:
x1+x2=-p; x1∙x2=q.
Выразим через p и q:
1) сумму квадратов корней уравнения x2+px+q=0;
2) сумму кубов корней уравнения x2+px+q=0.
Решение.
1) Выражение x12+x22 получится, если взвести в квадрат обе части равенства x1+x2=-p;
(x1+x2)2=(-p)2; раскрываем скобки: x12+2x1x2+ x22=p2; выражаем искомую сумму: x12+x22=p2-2x1x2=p2-2q. Мы получили полезное равенство: x12+x22=p2-2q.
2) Выражение x13+x23 представим по формуле суммы кубов в виде:
(x13+x23)=(x1+x2)(x12-x1x2+x22)=-p·(p2-2q-q)=-p·(p2-3q).
Еще одно полезное равенство: x13+x23=-p·(p2-3q).
Примеры.
3) x2-3x-4=0. Не решая уравнение, вычислите значение выражения x12+x22 .
Решение.
По теореме Виета сумма корней этого приведенного квадратного уравнения
x1+x2=-p=3, а произведение x1∙x2=q=-4. Применим полученное нами (в примере 1) равенство:
x12+x22=p2-2q. У нас -p=x1+x2=3 → p2=32=9; q=x1x2=-4. Тогда x12+x22=9-2·(-4)=9+8=17.
Ответ: x12+x22=17.
4) x2-2x-4=0. Вычислить: x13+x23.
Решение.
По теореме Виета сумма корней этого приведенного квадратного уравнения x1+x2=-p=2, а произведение x1∙x2=q=-4. Применим полученное нами (в примере 2) равенство: x13+x23=-p·(p2-3q)=2·(22-3·(-4))=2·(4+12)=2·16=32.
Ответ: x13+x23=32.
Вопрос: а если нам дано не приведенное квадратное уравнение? Ответ: его всегда можно «привести», разделив почленно на первый коэффициент.
5) 2x2-5x-7=0. Не решая, вычислить: x12+x22.
Решение. Нам дано полное квадратное уравнение. Разделим обе части равенства на 2 (первый коэффициент) и получим приведенное квадратное уравнение: x2-2,5x-3,5=0.
По теореме Виета сумма корней равна 2,5; произведение корней равно -3,5.
Решаем так же, как пример 3), используя равенство: x12+x22=p2-2q.
x12+x22=p2-2q=2,52-2∙(-3,5)=6,25+7=13,25.
Ответ: x12+x22=13,25.
6) x2-5x-2=0. Найти:
Преобразуем это равенство и, заменив по теореме Виета сумму корней через -p, а произведение корней через q, получим еще одну полезную формулу. При выводе формулы использовали равенство 1): x12+x22=p2-2q.
В нашем примере x1+x2=-p=5; x1∙x2=q=-2. Подставляем эти значения в полученную формулу:
7) x2-13x+36=0. Найти:
Преобразуем эту сумму и получим формулу, по которой можно будет находить сумму арифметических квадратных корней из корней квадратного уравнения.
У нас x1+x2=-p=13; x1∙x2=q=36. Подставляем эти значения в выведенную формулу:
Совет: всегда проверяйте возможность нахождения корней квадратного уравнения по подходящему способу, ведь 4 рассмотренные полезные формулы позволяют быстро выполнить задание, прежде всего, в тех случаях, когда дискриминант — «неудобное» число. Во всех простых случаях находите корни и оперируйте ими. Например, в последнем примере подберем корни по теореме Виета: сумма корней должна быть равна 13, а произведение корней 36. Что это за числа? Конечно, 4 и 9. А теперь считайте сумму квадратных корней из этих чисел: 2+3=5. Вот так то!
