С развитием науки и техники математикам понадобились большие массивы данных, которые обычно записывались в таблицу. Между элементами таблицы часто требовались определенные операции, например, надо было сложить сходные элементы двух разных таблиц, чтобы результат записать в третьей таблице. Затем работать уже с этой таблицей, оперируя и ее элементами. Сейчас же ученые оперируют тысячами таблиц. Понадобился математический аппарат для упрощенной работы с таблицами. Так появились матрицы. Математики назвали таблицы матрицами, классифицировали их, описали операции с матрицами, свойства и способы упрощенной работы с ними. Начнем с определения матрицы.
В школьном курсе математики матрицы используются для быстрого решения систем уравнений.
Содержание
Определение матрицы
Матрицей называют множество чисел, образующих прямоугольную таблицу, которая содержит m строк и n столбцов. Для записи матрицы используется следующее обозначение:

Для любого элемента ![]() первый индекс
первый индекс ![]() означает номер строки, а второй индекс
означает номер строки, а второй индекс ![]() — номер столбца. Сокращенно матрицу типа
— номер столбца. Сокращенно матрицу типа ![]() можно записать так:
можно записать так: ![]() , где
, где ![]() ;
; ![]() .
.
Диагонали матрицы
Диагональ матрицы, с совпадающими индексами элементов, при условии равенства ее строк и столбцов, называют главной диагональю матрицы.
Например, в матрице

главная диагональ содержит элементы ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Диагональ, которая содержит элементы ![]() ,
, ![]() , ...
, ... ![]() называется побочной диагональю матрицы. В матрице C эта диагональ представлена элементами
называется побочной диагональю матрицы. В матрице C эта диагональ представлена элементами ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Виды матриц
Матрицы бывают квадратными и прямоугольными, диагональными, скалярными, нулевыми, единичными, матрицы-столбцы и матрицы-строки. Дадим определение каждой матрице и рассмотрим их на примерах.
Прямоугольная матрица
Если число строк матрицы не равно числу столбцов ![]() , то матрица называется прямоугольной. Примеры прямоугольной матрицы
, то матрица называется прямоугольной. Примеры прямоугольной матрицы
 и
и

Квадратная матрица
Если число строк равно числу столбцов ![]() , тогда мы получаем квадратную матрицу. Примеры квадратных матриц:
, тогда мы получаем квадратную матрицу. Примеры квадратных матриц:

и

Число столбцов или строк квадратной матрицы указывает на ее порядок. Так, матрица А в нашем примере третьего порядка, а матрица B четвертого.
Нулевая матрица
Если все элементы в матрице равны нулю, то такая матрица называется нулевой матрицей. Например,
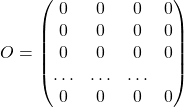
Нулевая матрица обозначается буквой ![]() .
.
Диагональная матрица
Квадратная матрица, у которой отличны от нуля только элементы главной диагонали, называется диагональной матрицей. Пример диагональной матрицы:
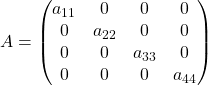
Диагональными матрицами являются, к примеру, такие:
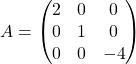
и
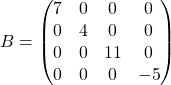
Скалярная матрица
Если у диагональной матрицы все числа на главной диагонали равны между собой, то матрица называется скалярной.
Например,
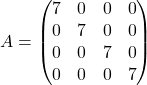
Единичная матрица
Если все числа в диагональной матрице, расположенные на главной диагонали, равны единице, то такая матрица называется единичной. Она записывается и обозначается так:
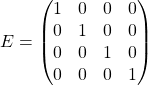
Матрица-строка
В прямоугольной матрице типа ![]() бывают такие случаи, когда m=1, тогда мы будем говорить о матрице-строке.
бывают такие случаи, когда m=1, тогда мы будем говорить о матрице-строке.
Пример:
![]()
Матрица-столбец
Прямоугольная матрица, у которой есть только один столбец, называется матрица-столбец. То есть матрица при n=1. Например:
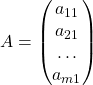
Матрицы-строки и матрицы-столбцы иначе называются векторами.









Круто про матрицы. Спасибо Вам.
Мне понравилось про матрицы. Спасибо.
Доходчиво.ю благодарю!