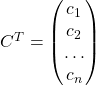Равенство матриц и транспонирование матриц

Мы изучили тему «Матрицы», дали определение матриц и рассмотрели основные виды матриц, теперь давайте введем понятие «равенство матриц», то есть определим, когда две матрицы являются равными.

Содержание

Определение равенства двух матриц

Матрицы называются равными, если они имеют одинаковое число строк и одинаковое число столбцов, а соответствующие элементы матриц равны: $a_{ij}=b_{ij}$ .

Таким образом, матрицы

$A=\begin{pmatrix} a_{11}& a_{12} & a_{13} & a_{14} \\ a_{21}& a_{22} & a_{23} & a_{24} \end{pmatrix}$

$B=\begin{pmatrix} b_{11}& b_{12} & b_{13} & b_{14} \\ b_{21}& b_{22} & b_{23} & b_{24} \end{pmatrix}$

равны, если $a_{11}=b_{11}$ , $a_{12}=b_{12}$ , $a_{13}=b_{13}$ , $a_{14}=b_{14}$ , $a_{21}=b_{21}$ , $a_{22}=b_{22}$ , $a_{23}=b_{23}$ , $a_{24}=b_{24}$ , $a_{31}=b_{31}$ , $a_{32}=b_{32}$ , $a_{33}=b_{33}$ , $a_{34}=b_{34}$ , $a_{41}=b_{41}$ , $a_{42}=b_{42}$ , $a_{43}=b_{43}$ , $a_{44}=b_{44}$ .

Равные матрицы имеют одинаковое строение, так как для неравных по строению матриц невозможно создать равенство $a_{ij}=b_{ij}$ .

Транспонирование матриц

Если в матрице типа $m \times n$ , имеющей вид

$A=\begin{pmatrix} a_{11}& a_{12} & \ldots & a_{1n} \\ a_{21}& a_{22} & \ldots & a_{2n} \\ \ldots & \ldots& \ldots & \ldots\\ a_{m1}& a_{m2} & \ldots & a_{mn} \end{pmatrix}$

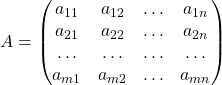
переставить строки со столбцами, получим матрицу, типа $n \times m$ , которая является транспонированной матрицей:

$A^{T}=\begin{pmatrix} a_{11}& a_{12} & \ldots & a_{m1} \\ a_{21}& a_{22} & \ldots & a_{m2} \\ \ldots & \ldots& \ldots & \ldots\\ a_{1n}& a_{2n} & \ldots & a_{mn} \end{pmatrix}$

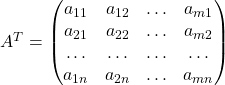
Если матрица состоит из одной строки (матрица-строка), то при транспонировании такая матрица становится матрицей-столбцом.

Свойства транспонирования матриц

Перечислим свойства транспонирования матриц, немного забежим вперед:

Если матрицу транспонировать дважды, то получится исходная матрица.
Транспонирование суммы матриц равно сумме транспонированных матриц.
Можно умножить исходную матрицу на число или уже транспонированную матрицу умножить на число, порядок умножения не важен. Таким образом, транспонированное произведение матрицы и числа равно произведению этого же числа на транспонированную матрицу.
Транспонированное произведение матриц равно произведению транспонированных матриц в обратном порядке

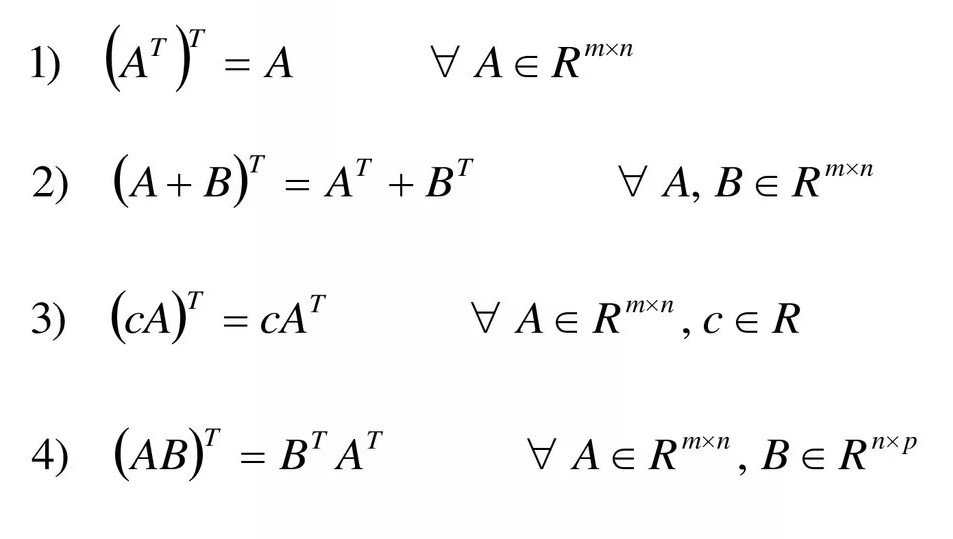
Транспонирование векторов

При транспонировании векторов матрица-столбец становится матрицей-строкой, а матрица-строка становится матрицей-столбцом. Так, например, матрица-строка

$C=\begin{pmatrix} c_{1}& c_{2} & c_{3} & ... & c_{n} \end{pmatrix}$