Как умножить матрицу на матрицу и как умножить матрицу на число — обсуждаем на примерах с решением и объяснением. Произведение матрицы на число и произведение матрицы на матрицу просто и на примерах.
Содержание
Умножение матрицы на число
Произведением матрицы ![]() на число
на число ![]() называется такая матрица
называется такая матрица ![]() , каждый элемент которой равен
, каждый элемент которой равен ![]() , то есть, если
, то есть, если
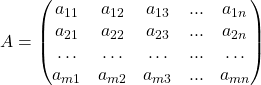 ,
,
то
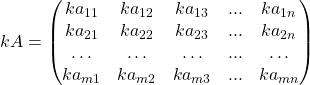 .
.
Рассмотрим умножение матрицы на число на примере:
Пример 1
Умножьте матрицу ![]() на число
на число ![]() .
.
Решение: Чтобы умножить матрицу ![]() на число 2, нужно умножить на это число каждый элемент матрицы. Итак, получим:
на число 2, нужно умножить на это число каждый элемент матрицы. Итак, получим:
![]() .
.
Пример 2
Найдите матрицу, противоположную матрицу 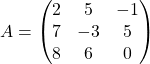 .
.
Решение: Чтобы найти противоположную матрицу надо умножить исходную матрицу на ![]() .
.
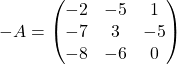 .
.
Пример 3
Даны матрицы 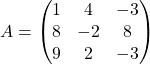 и
и 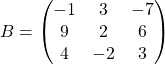 . Вычислите
. Вычислите ![]() .
.
Решение:
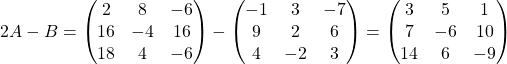 .
.
Умножение матрицы на матрицу
Чтобы умножить матрицу на матрицу необходимо умножать последовательно каждый элемент каждой строки первой матрицы на каждый элемент каждого столбца второй матрицы и сумму этих произведений записать в соответствующем элементе матрицы-произведения.
Давайте рассмотрим умножение матрицы на матрицу на примере. Пусть нам нужно умножить две квадратные матрицы ![]() и
и ![]() .
.
 ,
, 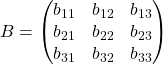
Умножением матрицы на матрицу называется матрица:
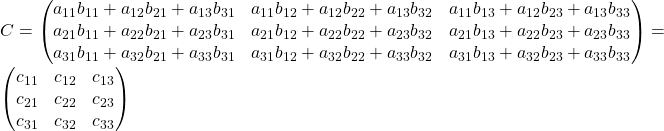 .
.
Таким образом, получаем:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Рассмотрим умножение матрицы на матрицу на примерах.
Пример 1
Найдите произведение матриц:
![]() и
и ![]() .
.
Решение:
Находим произведение матриц ![]() .
.
Таким образом, для прямоугольных матриц правило умножения матрицы на матрицу такое же, как и для квадратных матриц.
Пример 2
Найдите произведение AB, если
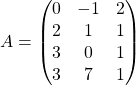 ,
, 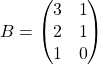 .
.
Решение:
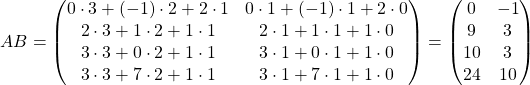 .
.
Мы смогли найти произведение AB, однако, мы не сможем найти произведение BA.
Правила умножения матриц
Не все матрицы можно перемножать, для того, чтобы произведение матриц было возможным, необходимо соблюдение следующих правил:
Умножение матрицы A на матрицу B имеет смысл только в том случае, когда число столбцов матрицы A равно числу строк матрицы B.
В результате умножения двух прямоугольных матриц получается матрица, содержащая столько строк, сколько строк в первой матрице, и столько столбцов, сколько столбцов во второй матрице.
Свойства умножения матриц
Рассмотрим умножение двух матриц ![]() и
и ![]() . Найдем произведение
. Найдем произведение ![]() и произведение
и произведение ![]() , а затем сравним эти произведения.
, а затем сравним эти произведения.
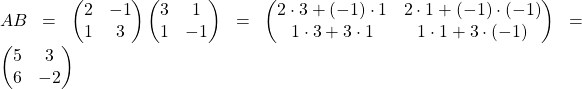 ;
;
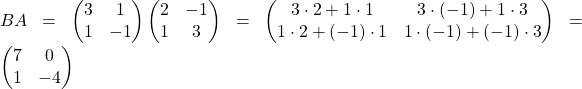 .
.
Очевидно, что ![]() . Таким образом, для произведения матриц переместительный закон не выполняется. Однако, два других закона умножения, сочетательный закон и распределительный закон выполняются:
. Таким образом, для произведения матриц переместительный закон не выполняется. Однако, два других закона умножения, сочетательный закон и распределительный закон выполняются:
![]() — сочетательный закон умножения,
— сочетательный закон умножения,
![]() — распределительный закон.
— распределительный закон.
Из школьного курса математики известно, что произведение двух отличных от нуля чисел равно отличному от нуля числу. Однако при умножении двух ненулевых матриц можно получить нулевую матрицу, смотрите:
Возьмем две матрицы ![]() и
и ![]() . Найдем произведение этих матриц:
. Найдем произведение этих матриц:
![]()
Вот такими удивительными свойствами обладает умножение матриц.
Читайте еще статьи про матрицы:
- Матрицы и определение матриц, виды матриц
- Равенство матриц и транспонирование матрицы
- Сложение матриц и вычитание матриц
- Основные свойства определителей матрицы
- Умножение матрицы на матрицу и умножение матрицы на число
- Определитель матрицы








Вот тут ок.