Определение: параллелограмм — это четырехугольник, у которого противолежащие стороны попарно параллельны, является геометрической фигурой.
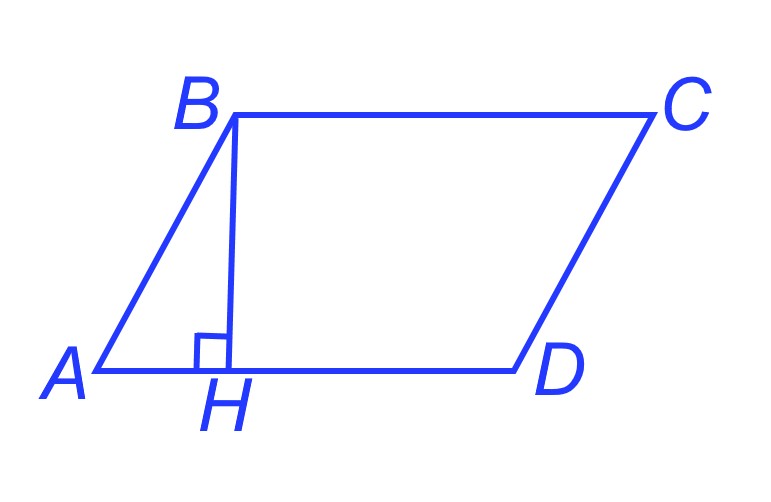
Высотой параллелограмма называется перпендикуляр, опущенный из его вершины на прямую, содержащую противолежащую ей сторону. В этой статье мы рассмотрим основные свойства параллелограмма и решим задачи, с опорой на эти свойства.
Изучение этой геометрической фигуры начинается в 8 классе, однако знакомство с ней происходит еще в дошкольный период, например, когда мы видим этот четырехугольник в элементах конструктора, а можем сами получить такую фигуру, если прикрепить стороны прямоугольника не крепко и потянуть за одну из них, тогда перпендикулярность сторон нарушится и мы получим тот четырехугольник, который будем сегодня с вами изучать. Этот четырехугольник настолько популярен, что часто встречается в орнаментах и даже есть на флагах некоторых государств, например, на флаге острова Саба — островного государства в Карибском море.
Содержание
Свойства параллелограмма
Свойство 1
Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.
Доказательство.
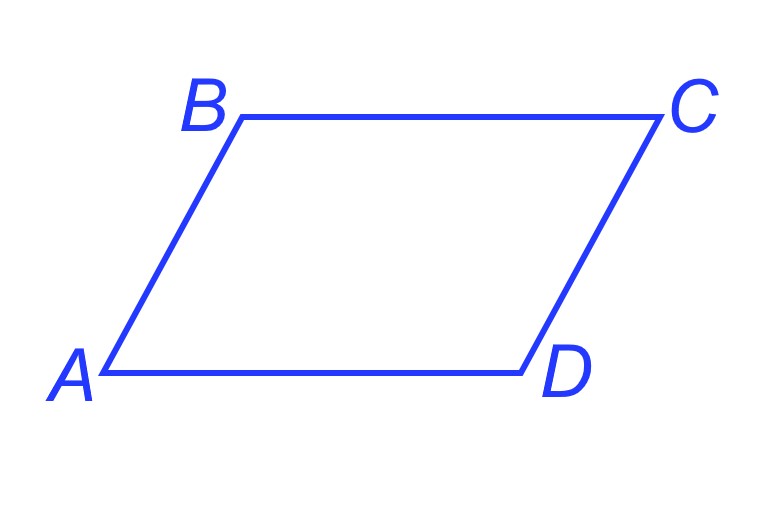
Рассмотрим параллелограмм ABCD. Докажем, например, что сумма ∠A и ∠B, прилежащих к стороне AB, равна 180°.
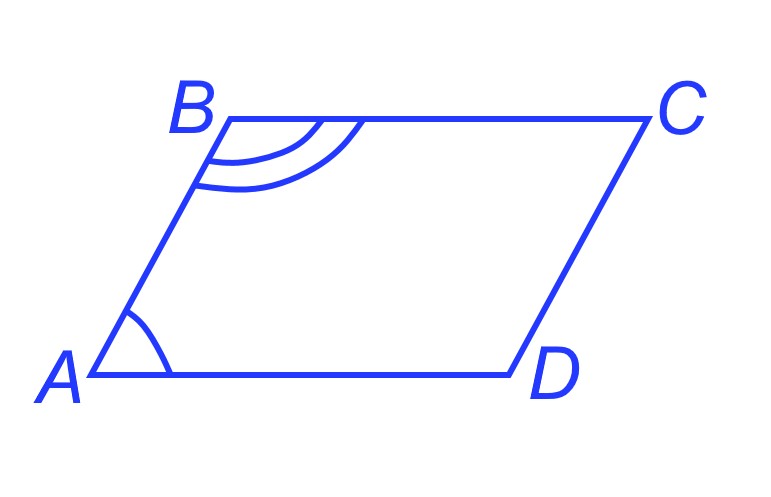
Действительно, ∠A и ∠B являются внутренними односторонним углами при параллельных прямых АD, BC и секущей AB. В седьмом классе доказывалось, что если две параллельные прямые пересечены третьей прямой, то внутренние односторонние углы составляют в сумме 180°. Следовательно, сумма ∠А +∠B=180°. Аналогичным образом доказывается, что суммы углов параллелограмма, прилежащих к другим его сторонам, также равны 180°.
Свойство 2
У параллелограмма противоположные стороны равны и противолежащие углы равны.
Доказательство.
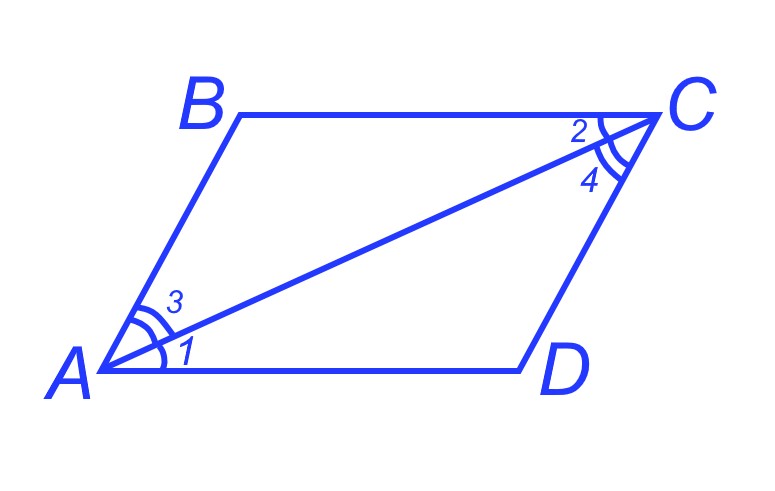
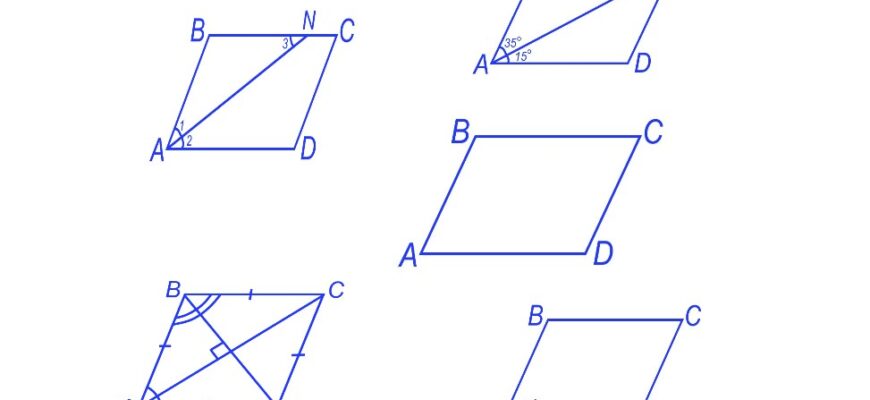
Рассмотрим параллелограмм ABCD. Диагональ АС разбивает его на два треугольника АВС и CDA. Эти треугольники равны по второму признаку равенства треугольников (AC — общая сторона, ∠1=∠2, ∠3=∠4 как внутренние накрест лежащие углы при двух параллельных прямых и секущей.) Из равенства треугольников следует, что AB=CD, BC=AD и ∠B=∠D. Кроме того, ∠A=∠1+∠3=∠2+∠4=∠C.
Свойство 3
Диагонали параллелограмма в точке пересечения делятся пополам.
Доказательство.
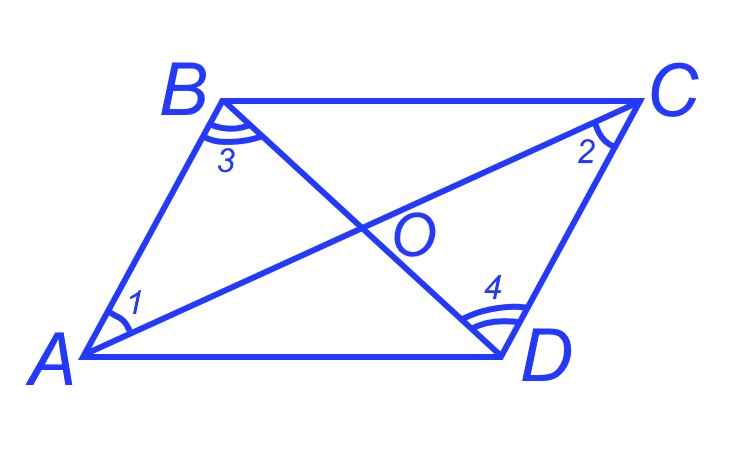
Рассмотрим параллелограмм ABCD. Обозначим O точку пересечения диагоналей AC и BD. Треугольники AOB и COD равны по второму признаку равенства треугольников (AB=CD, ∠1=∠2, ∠3=∠4 как внутренние накрест лежащие углы при двух параллельных прямых и секущей).
Из равенства треугольников следует равенство сторон AO=OC и DO=OB. То есть диагонали точкой пересечения делятся пополам. Что и требовалось доказать.
Неправильно
В геометрии важно не только построение фигур, но и произношение их названий. Так правильно следует говорить «параллелограмм» (с двумя «л» в первом случае и с двумя «м» в конце). Неправильно писать и говорить: паралеллограм, паралелограм, в паралелограми.
Математика требует четкости во всем.
Примеры решения задач
Решим несколько задач
Задача 1
У параллелограмма две стороны равны 30 и 40 см, найдите две другие стороны.
Решение.
По второму свойству стороны данной геометрической фигуры равны, нам даны два разных числа, значит, это не противоположные стороны, а смежные. Смежные стороны четырехугольника — это те стороны, которые прилежат к одной вершине. Таким образом, мы можем сказать, что две другие стороны также будут 30 и 40 см.
Ответ: 30 см, 40 см.
Задача 2
Один из углов параллелограмма равен 45°. Найдите остальные углы параллелограмма?
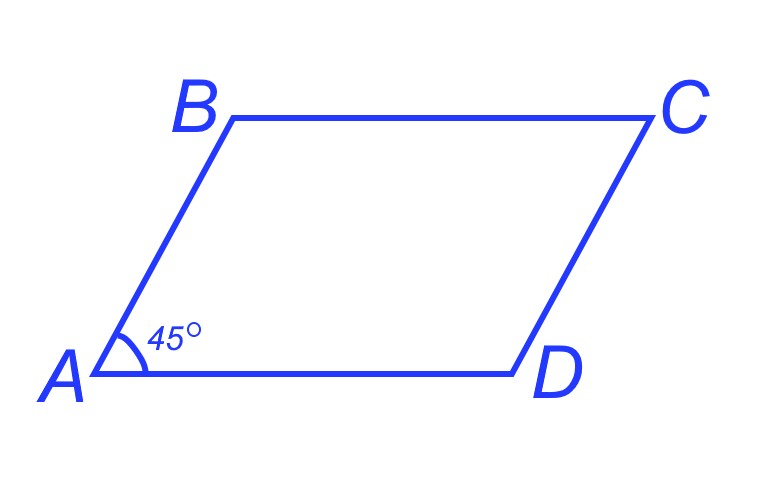
Решение: Согласно первому свойству углы при одной стороне в сумме дают 180°. А также противоположные углы равны по второму свойству. Таким образом, ∠A= ∠C=45° и ∠B=∠D=180°- 45°=135°.
Ответ: 45°, 135°, 135°.
Задача 3
Диагональ параллелограмма образует с двумя его сторонами углы 15° и 35°. Найдите остальные его углы.
Решение:
Сделаем чертеж. Итак, диагональ AC делит ∠A на две части, по 15 и 35 градусов.
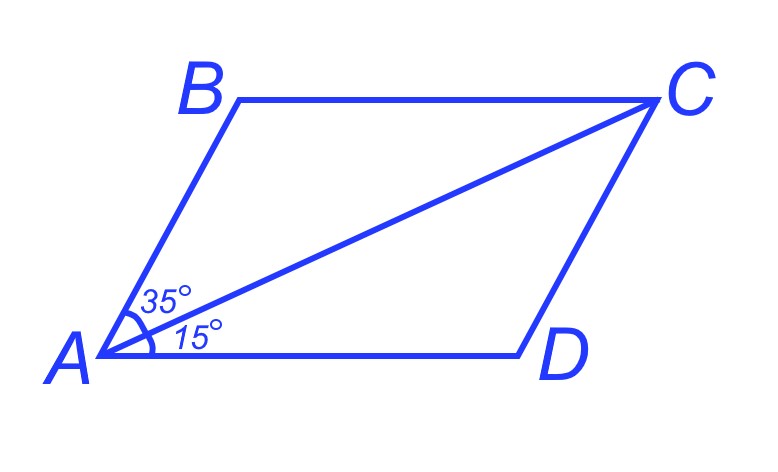
Вместе получается 15+35=50 градусов. Тогда противоположный ∠C тоже будет 50 градусов по второму свойству (о равенстве сторон и противоположных углов). Так как сумма внутренних углов при одной стороне 180°, то найдем: ∠B=180°-∠A=180°-50°=130°.
Таким образом, ∠D = 130°.
Ответ: 50°, 130°, 50°, 130°.
Задача 4
Найдите углы параллелограмма, если известно, что один из его углов больше другого на 20º.
Решение:
Пусть ∠A будет x, тогда ∠B= x+20. Известно, что ∠A и ∠B в сумме дают 180°. Составим уравнение:
x+x+20=180
2x+20=180
2x=180-20
2x=160
x=80
Таким образом, один ∠A= 80°, а ∠B=100°. По второму свойству имеет ∠C=80° и ∠D=100°.
Ответ: 80°, 80°, 100°, 100°
Задача 5
Найдите стороны параллелограмма, если его периметр равен 48 см, а одна из его сторон больше другой на 4 см.
Решение:
Пусть одна сторона равна x см, тогда другая сторона x+4. Периметр — это сумма всех сторон, а стороны в данной геометрической фигуре попарно равны по второму свойству. Составим уравнение: 2 (x+x+4)= 48. Решим это уравнение:
2x+4=24
2x=20
x=10
Значит, одна сторона 10 см, а другая сторона будет 10+4=14 см.
Ответ: 10 см и 14 см.
Задача 6
Докажите, что биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
Доказательство:
Нарисуем параллелограмм ABCD, и проведем биссектрису ∠A. Точку пересечения биссектрисы и стороны BC обозначим N. Требуется доказать, что треугольник ABN равнобедренный.
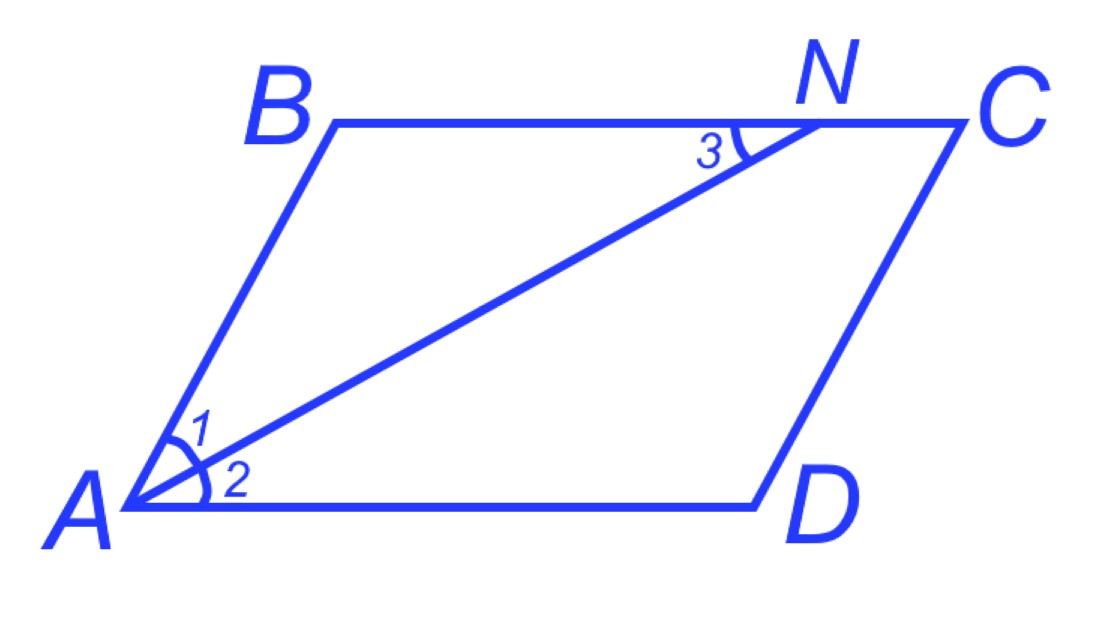
У равнобедренного треугольника две стороны равны и углы при основании равны. Так как AN биссектриса, то ∠1=∠2 и ∠2=∠3 (как внутренние накрест лежащие углы), отсюда ∠3=∠1. Таким образом, треугольник ABN равнобедренный.
Из того, что треугольник равнобедренный следует, что AB=BN. Это можно будет использовать при решении других подобных задач.
Что и требовалось доказать.
Частный случай параллелограмма
Частным случаем параллелограмма является ромб.
Ромб — это параллелограмм, у которого все стороны равны. Свойства ромба такие же как и свойства параллелограмма. Но есть и особенность — диагонали ромба перпендикулярны и являются биссектрисами его углов.
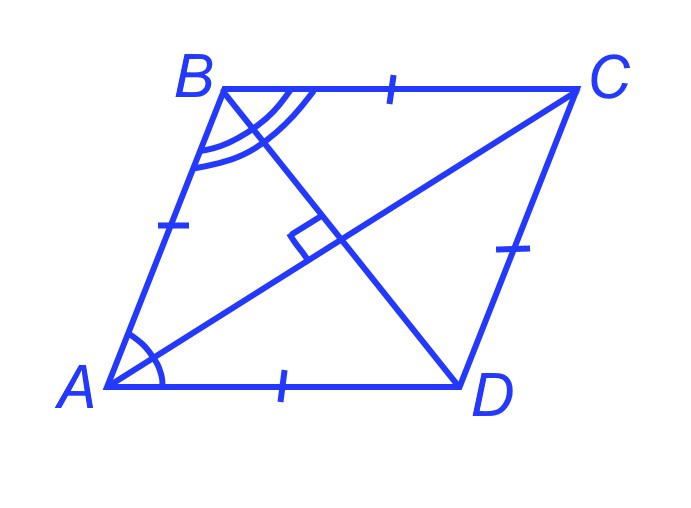
Изучением ромба мы займемся подробно в следующих статьях, а также докажем это свойство ромба о его диагоналях.
Заключение
В геометрии 8 класса о параллелограмме можно узнать — определение, свойства и по каким признакам определить, что перед вами именно эта геометрическая фигура. Например, нам дана такая задача — определите четырехугольник, если его диагонали пересекаются в точке O, которая делит их пополам и стороны данного четырехугольника попарно параллельны, то понятно о какой фигуре здесь идет речь. О вписанных и описанных окружностях в такой четырехугольник вы узнаете в девятом классе.
Свойства надо выучить, необязательно запоминать их порядок, главное знать содержание, уметь использовать в решении геометрических задач.