В алгебре часто решаются задачи на нахождение площади криволинейной трапеции, заключенной между двумя кривыми. В задачах обычно спрашивают как найти площадь криволинейной трапеции ограниченной прямыми или как вычислить площадь фигуры, ограниченной линиями. Вычисление площадей криволинейных трапеций изучается в курсе алгебры в 11 классе.
Криволинейная трапеция — это условное название фигур — областей, которые образуются графиком кривой и линиями ограничивающими график с двух сторон.
Различают два случая:
- Переменная интегрирования х;
- Переменная интегрирования у.
Рассмотрим оба этих случая.
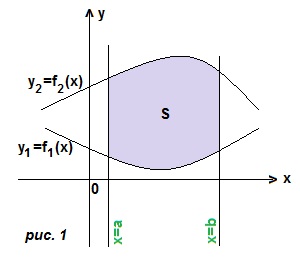
1) переменная интегрирования х. В этом случае трапеция ограничена сверху и снизу двумя кривыми, а слева и справа прямыми х=а, х=b. (рис. 1). Границы интегрирования a и b, а чтобы получить подынтегральную функцию, мы из уравнения верхней линии вычитаем уравнение нижней линии. Тогда площадь трапеции:
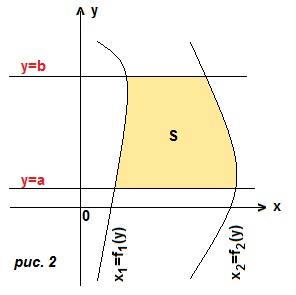
2) переменная интегрирования у. Криволинейная трапеция ограничена справа и слева двумя кривыми, а снизу и сверху прямыми y=a, y=b. (рис. 2). Границы интегрирования a и b. Чтобы получить подынтегральное выражение, мы из уравнения правой линии вычтем уравнение левой линии. Тогда площадь трапеции:![]()