Показательные уравнения, сводящиеся к квадратным

Разберем показательные уравнения, сводящиеся к квадратным. Их могут ученики кратко называть «квадратные показательные уравнения», хотя это название не точное. Однако, многие показательные уравнения заменой переменной сводятся к квадратному уравнению вида: ax²+bx+c=0.

Показательные уравнения, приводимые к квадратным на примерах

Уравнение 1

Решить уравнение:

1) 4^x+2^x+1-3=0. Представим 4^x в виде степени с основанием 2.

(2²)^x+2^x∙2¹-3=0; при возведении степени в степень основание оставляют, а показатели перемножают: 2·х=х·2, поэтому:

(2^x)²+2∙2^x-3=0;

вводим новую переменную: пусть 2^x=y;

y²+2y-3=0.

Дискриминант для четного второго коэффициента: D₁=1²-1∙(-3)=1+3=4=2² – полный квадрат, поэтому применим теорему Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

y₁+y₂=-2, y₁∙y₂=-3. Подбираем корни: y₁=-3, y₂=1.

Возвращаемся к переменной х:

1) 2^x=-3, нет решений, так как значения показательной функции: Е(у)=(0; +∞). (только положительные числа).

2) 2^x=1. Число 1 можно представлять в виде нулевой степени по любому основанию.

2^x=2⁰;

x=0.

Ответ: 0.

Уравнение 2

2) 0,25^2x-5∙0,5^2x+4=0.  Решаем аналогично. Представляем 0,25^2x— в виде степени с основанием 0,5.

(0,5²)^2x-5∙0,5^2x+4=0;

(0,5^2x)²-5∙0,5^2x+4=0.

0,5^2x=y; ввели новую переменную у и получили приведенное квадратное уравнение:

y²-5y+4=0;

Дискриминант D=b²-4ac=5²-4∙1∙4=25-16=9=3² — полный квадрат, применяем теорему Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

y₁+y₂=5, y₁+y₂=4. Корни приведенного квадратного уравнения находим подбором: y₁=1, y₂=4 и возвращаемся к переменной х:

1) 0,5^2x=1; число 1 можно представлять в виде нулевой степени по любому основанию.

0,5^2x=0,5⁰;

2x=0;

x=0.

2) 0,5^2x=4; приведем степень  0,5^2x  к основанию 2, применив формулу:   (1/a)^x =а^-х 

(¹/₂)^2x=2²;

2^-2x=2²; приравниваем показатели:

— 2x=2 |:(-2)

x=-1.

Ответ: -1; 0.

Уравнение 3

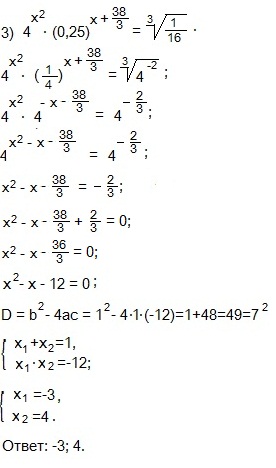
Представим левую и правую части в виде степеней с основанием 4, используя формулы: а^-х=1/a^x  и  a^x∙a^y=a^x+y .

Если равны две степени с одинаковыми основаниями, то основания можно опустить и приравнять показатели степеней. Переносим дробь из правой части равенства в левую и упрощаем левую часть.

Находим дискриминант приведенного квадратного уравнения. Дискриминант является квадратом целого числа, поэтому, подбираем корни, пользуясь теоремой Виета:  сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Итак, решение показательных уравнений, которое мы разбирали в предыдущем уроке, пополнилось еще одним методом — приведением показательного уравнения к обычному квадратному уравнению. Такие уравнения называют — показательные уравнения, сводящиеся к квадратным.