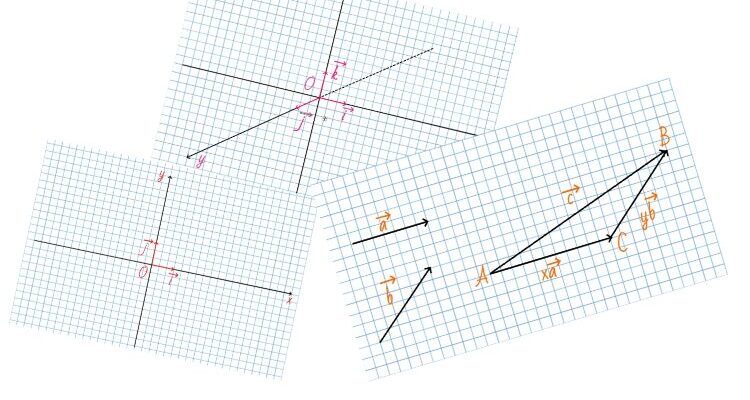
Представление вектора \vec{c} в виде \vec{c}=x \vec{a}+y \vec{b}, где векторы \vec{a} и \vec{b} являются неколлинеарными векторами, называется разложением вектора по двум неколлинеарным векторам.
Теорема (о разложении вектора по двум неколлинеарным векторам)
Теорема. Любой вектор с можно единственным образом представить в виде \vec{c}=x \vec{a}+y \vec{b}, где \vec{a} и \vec{b} — неколлинеарные векторы, х и у — числа.
Коллинеарные вектора \vec{m} и \vec{n} — это такие вектора, где один из векторов параллелен другому и связан с ним соотношением
\vec{m}=k\vec{n}
Доказательство:
Пусть даны векторы \vec{c}=\overrightarrow{AB}, \vec{a} и \vec{b}. Проведем через точки A и B прямые, параллельные векторам \vec{a} и \vec{b}, и обозначим точку C их пересечения. Тогда \overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{CB}.
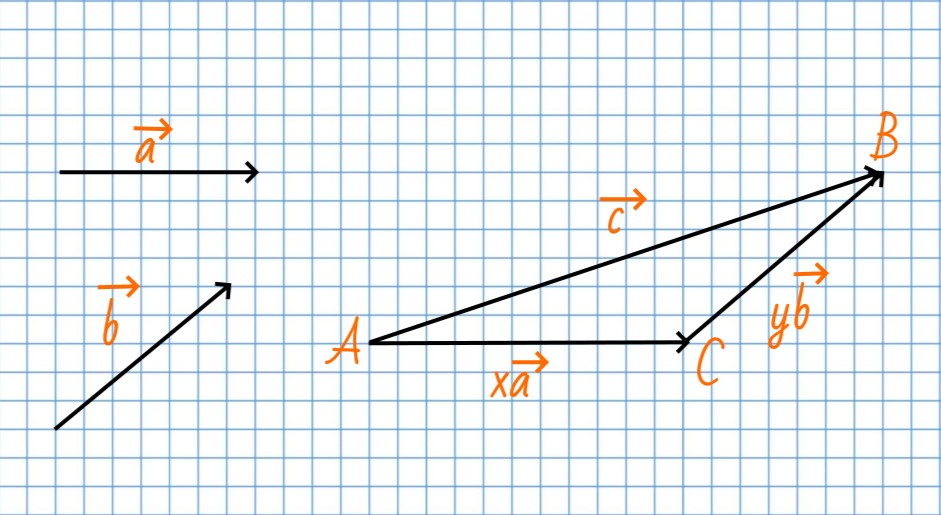
Так как векторы \vec{a} и \overrightarrow{AC} коллинеарные, то существует такое число х, что \overrightarrow{AC} =х\vec{a}. Векторы \vec{b} и \overrightarrow{CB} тоже коллинеарные, следовательно, существует такое число у, что \overrightarrow{CB} =y\vec{b}.
Таким образом, \vec{c}=x \vec{a}+y \vec{b}.
Докажем единственность такого представления вектора с способом от противного. Допустим, что имеется другое разложение вектора, например, такое:
\vec{c}=n \vec{a}+m \vec{b}, тогда два разложения вектора \vec{c} можно приравнять:
n \vec{a}+m \vec{b}=x \vec{a}+y \vec{b} (если равны левые части равенств, то равны и правые).
Перенесем все в левую часть равенства:
n \vec{a}+m \vec{b}-x \vec{a}-y \vec{b}=0
(n-x)\vec{a}+(m-y) \vec{b}=0
\displaystyle \vec{a}=\frac{y-m}{n-x} \vec{b}
То есть векторы \vec{a} и \vec{b} получаются коллинеарными. А у нас условие — векторы \vec{a} и \vec{b} — неколлинеарные вектора.
Таким образом, возможно только единственно возможное представление вектора \vec{c} в виде \vec{c}=x \vec{a}+y \vec{b}, где векторы \vec{a} и \vec{b} являются неколлинеарными векторами.
Теорема доказана.
Если вектор \vec{c} коллинеарен какому-либо из векторов \vec{a} и \vec{b}, то либо число x, либо число y равно нулю.
Базис векторов и разложение вектора по базису
В декартовой системе координат Oxy вектор с координатами (x, y) можно разложить по единичным векторам \vec{e_1}(1;0) и \vec{e_2}(0;1).
Тогда, например, вектор \vec{c}(3; -1) можно представить в виде разложения:
\vec{c}=x \vec{e_1}+y \vec{e_2}=3 \vec{e_1}-1 \vec{e_2}
Действительно:
\begin{cases} 3=3 \cdot 1+(-1)\cdot 0, \\ — 1=3 \cdot 0+(-1)\cdot 1. \end{cases}
Система векторов, по которым можно разложить вектор с коэффициентами разложения равными его координатам, называется базисом вектора. Вектора базиса всегда не коллинеарные. Координаты вектора будут верны только в отношении данного базиса.
Однако, это не отменяет тот факт, что вектор можно разложить и по другим векторам, то есть по новому базису. Тогда говорят о переходе к новому базису векторов.
Обычно в декартовой системе координат базисные векторы на плоскости обозначают так: \vec{i}(1;0) и \vec{j}(0;1).
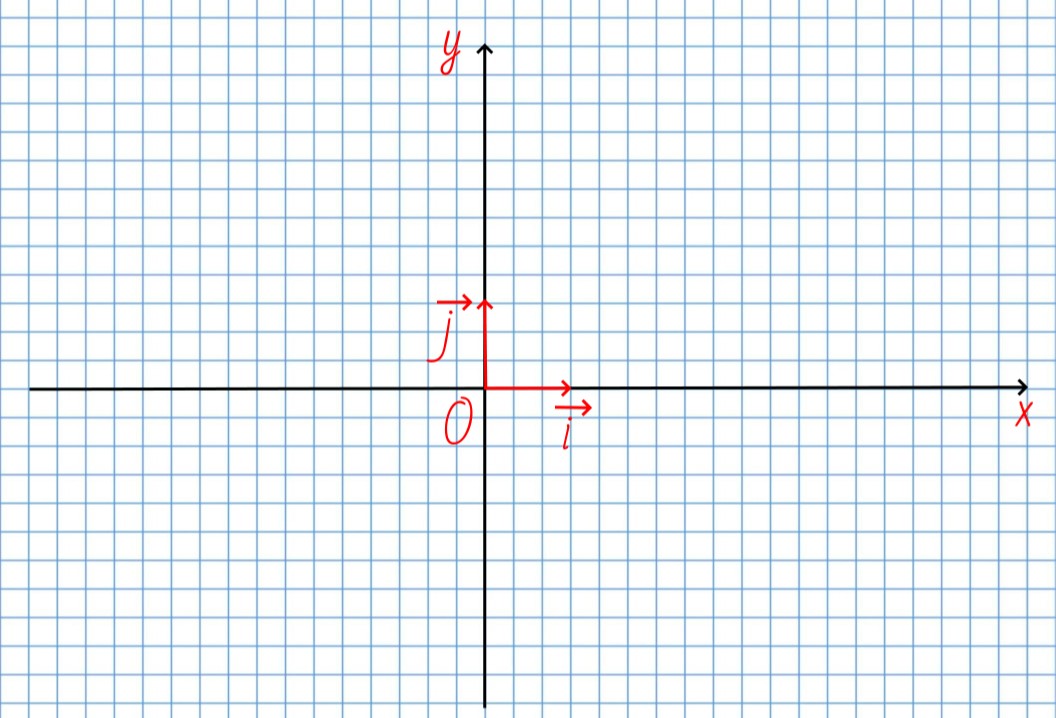
В пространственной декартовой системе координат базис векторов будет: \vec{i}(1; 0; 0), \vec{j}(0;1; 0), \vec{k}(0;0;1)
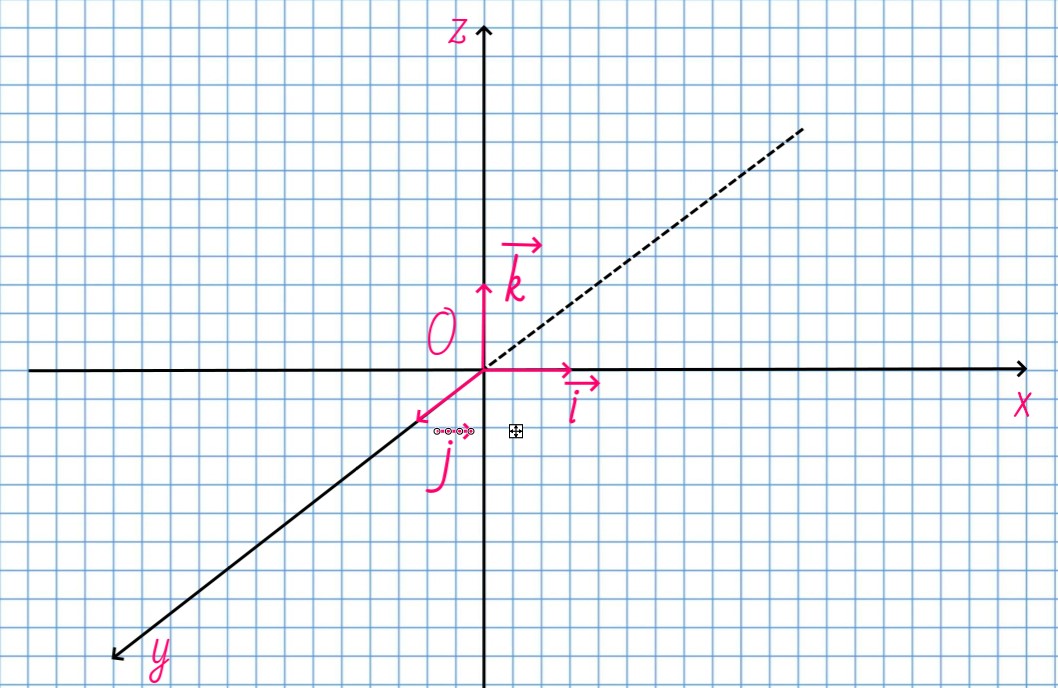
В то же время на любых векторах можно построить свою систему отсчета, тогда данные вектора будут считаться базисом этой системы и в этой системе можно найти координаты любого вектора. То есть любой вектор можно разложить по базису, конечно, если при этом базисные вектора не являются коллинеарными.
Примеры разложения вектора
Пример 1. Разложить вектор \vec{c}(0; 1) по двум векторам \vec{a}(3; 6) и \vec{b}(4; 9).
Решение:
Для разложения вектора \vec{c} запишем:
\vec{c}=x \vec{a}+y \vec{b}
Нам нужно найти коэффициенты разложения x и y, для этого разложим каждую координату вектора \vec{c}:
- Для абсциссы: 0=x \cdot 3+y \cdot 4
- Для ординаты: 1=x \cdot 6+y \cdot 9
Получаем систему из двух уравнений с двумя неизвестными, которую решаем:
\begin{cases} 3x+4y=0, \\ 6x+9y=1. \end{cases}
Решая, получаем: \displaystyle x=\frac{-4}{3} и y=1
И разложение вектора \vec{c} будет иметь вид: \displaystyle \vec{c}=-\frac{4}{3} \vec{a}+\vec{b}
Пример 2. Найти координаты вектора \vec{a} в базисе, если известно разложение вектора по базису \vec{e_1} и \vec{e_2}:
\vec{a}=7 \vec{e_1}+5 \vec{e_2}
Решение: Координаты вектора в базисе векторов \vec{e_1} и \vec{e_2} будут равны коэффициентам разложения, то есть \vec{a}(7; 5)
Ответ: \vec{a}(7; 5)
Пример 3. Разложить вектор \vec{b}(1; 2) по базису \vec{e_1}(2; 3) и \vec{e_2}(2; 5).
Решение:
Запишем разложение вектора по базису:
\vec{b}=b_1 \vec{e_1}+b_2 \vec{e_2}
Получим систему уравнений:
\begin{cases} 1=2b_1+4b_2, \\ 2=2b_1+5b_2. \end{cases}
От второго уравнения системы отнимем первое, получим:
\begin{cases} 1=b_2, \\ 2=2b_1+5b_2. \end{cases}
Тогда:
\begin{cases} b_2=1, \\ b_1=-1,5. \end{cases}
И разложение вектора будет иметь вид: \vec{b}=-1,5 \vec{e_1}+\vec{e_2}