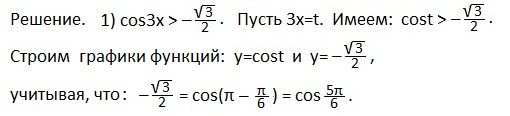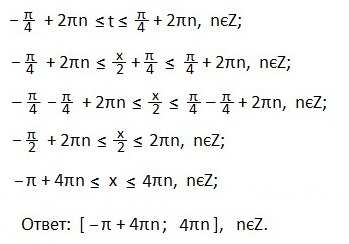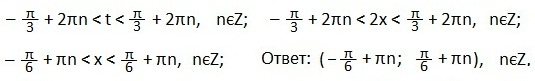На предыдущих трех занятиях по решению тригонометрических неравенств графическим способом мы рассмотрели неравенства вида:
- sint < a («10.2.1. Решение тригонометрических неравенств. Часть 1.»)
- sint > a («10.2.2. Решение тригонометрических неравенств. Часть 2.»)
- cost < a («10.2.3. Решение тригонометрических неравенств. Часть 3.»)
Рассмотрим тригонометрические неравенства вида: cost > a.
Используем алгоритм решения, как в предыдущем уроке 10.2.3. Решение тригонометрических неравенств. Часть 3.
1. Если аргумент — сложный (отличен от х), то заменяем его на t.
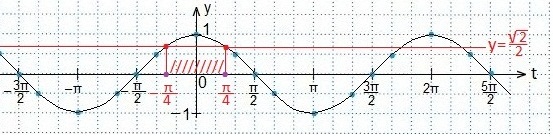
2. Строим в одной координатной плоскости tOy графики функций y=cost и y=a.
3. Находим такие две соседние точки пересечения графиков, между которыми синусоида располагается выше прямой у=а. Находим абсциссы этих точек.
4. Записываем двойное неравенство для аргумента t, учитывая период косинуса (t будет между найденными абсциссами).
5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.
Решение тригонометрических неравенств с помощью графиков надежно страхует нас от ошибок только в том случае, если мы грамотно построим синусоиду. (График функции y=cosx также называют синусоидой!) Построение синусоиды y=cosx рассматривается подробно в предыдущем уроке 10.2.3. Решение тригонометрических неравенств. Часть 3.
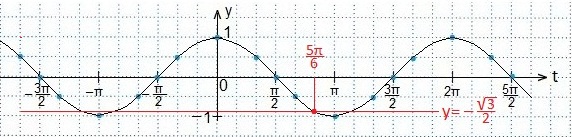
Пример 1
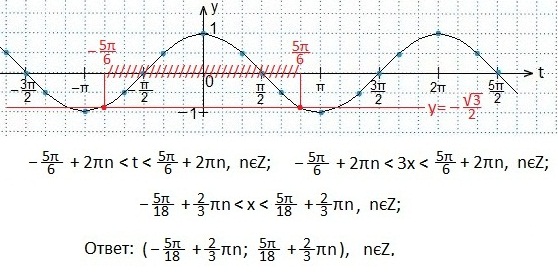
Далее, по алгоритму, определяем те значения аргумента t, при которых синусоида располагается выше прямой. Выпишем эти значения в виде двойного неравенства, учитывая периодичность функции косинуса, а затем вернемся к первоначальному аргументу х.
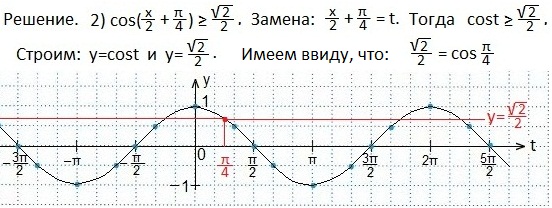
Пример 2
Выделяем промежуток значений t, при которых синусоида находится выше прямой.
Записываем в виде двойного неравенства значения t, удовлетворяющих условию. Не забываем, что наименьший период функции y=cost равен 2π. Возвращаемся к переменной х, постепенно упрощая все части двойного неравенства.
Ответ записываем в виде закрытого числового промежутка, так как неравенство было нестрогое.
Пример 3
Нас будет интересовать промежуток значений t, при которых точки синусоиды будут лежать выше прямой.
Значения t запишем в виде двойного неравенства, перезапишем эти же значения для 2х и выразим х. Ответ запишем в виде числового промежутка.
Смотрите видео: «10.2.4. Решение тригонометрических неравенств. Часть 4.»
И снова формула, которой вам следует воспользоваться на экзамене ЕНТ или ЕГЭ при решении тригонометрического неравенства вида cost > a.
Если cost > a, (-1≤а≤1), то - arccos a + 2πn < t < arccos a + 2πn, nєZ.
Применяйте формулы для решения тригонометрических неравенств, и вы сэкономите время на экзаменационном тестировании.